Definition

Central Limit Theorem (CLT): the distribution of sample statistics is nearly normal, centered at the population mean, and with a standard deviation equal to the population standard deviation divided by sqrt(n).

                      σ
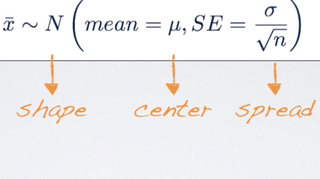
x̄ ~ N (mean = μ, SE = - )
                     √n
 
N stand for Normal Distribution
SE stand for Standard Error
μ is the population mean
σ is the population standard deviation
n is sample size

This is called Central Limit Theorem because it is central to much of the statistical inference theory. So, the CLT tells us about

• - the shape, which it says that is going to be nearly normal.
• - the center, which it says that the sampling distribution is going to be centered at the population mean.
• - the spread, it is the spread of the sampling distribution, which we measure using the standard error.

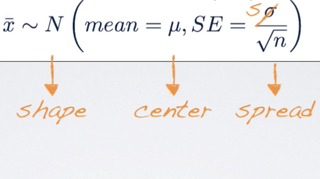
If σ (σ is the population SD) is unknown, we use S, the sample SD, to estimate the standard error.

Note: σ is often unknown because we don't have access to the entire population to calculate σ

For a sample statistic - the mean, the sampling distributions of the mean, distribution of sample means from many samples, is nearly normal,

Conditions

Certain conditions must be met for the Central Limit Theorem to apply. There are

1. Independence;
2. Sample size/skew;

Independence

The sampled observations must be independent. And this is very difficult to verify, but it is more likely, if we have used random sampling or assignment, depending on whether we have an observational study, where we're sampling from the population, randomly, or we have an experiment where we're randomly assigning experimental units to various treatments.

And if sampling without replacement, n < 10% of the population

Sample size/skew

The other condition is related to the sample size or skew. Either the population distribution is normal, or if the population distribution is skewed, or we have no idea what it looks like, the sample size is large. According to the CLT, if the population distribution is normal, the sampling distribution will also be nearly normal, regardless of the sample size. However, if the population distribution is not normal, the more skewed the population distribution, the larger sample size we need for the CLT to apply. For moderately skewed distributions, n > 30 is a widely used rule of thumb.

This distribution of the population is also something very difficult to verify because we often do not know what the population looks like.

Reference & Resources

• N/A