Disjoint Events

Disjoint Events, by definition, can not happen at the same time. A synonym for this term is mutually exclusive.

For example:

• The outcome of a single coin toss can not be a head and a tail.
• A student can not both fail and pass a class.
• A single card drawn from a deck can not be an ace and a queen at the same time.

In probability, disjoint event A and B is expressed as:

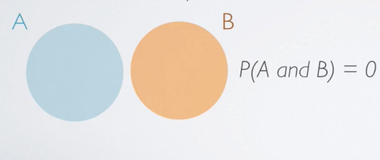
P(A and B) = 0

In Venn diagram representation, we represent each event by the circles, if event A and B are disjoint, we end up with two circles that don't touch each other.

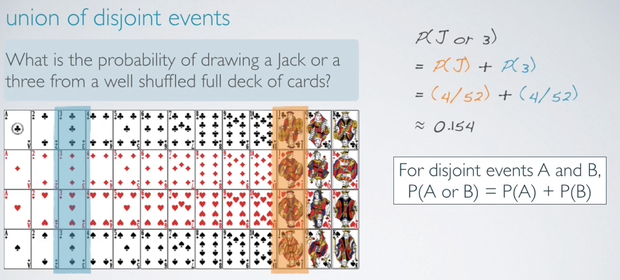
Union of disjoint events

For disjoint events A and B, the probability of A or B happening is simply the probability of A plus the probability of B.

P(A or B) = P(A) + P(B)

Non-disjoint Events

Non-disjoint events, on the other hand, can happen at the same time.

For example:

• A student can get an A in Stats and A in History at the same time.

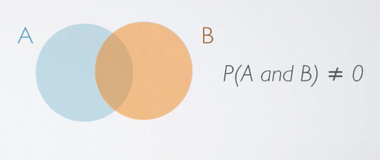
In Venn diagram representation of events A and B that are non-disjoint, we have two circles that overlap, or in other words, join, which indicates that the probability of event A and B happening at the same time is non-zero. So it is some number between 0 and 1.

P(A and B) ≠ 0

Union of non-disjoint events

For non-disjoint events A and B, the probability of A or B happening is the P(A) plus P(B) minus the probability of A and B happening at the same time (Avoid double counting) .

P(A or B) = P(A) + P(B) - P(A and B)

Sample Space

A sample space is a collection of all possible outcomes of a trial.

For example:

A couple has two kids, the sample space for the sex of these 2 kids is:

S = {MM, FF, FM, MF}
M for Male, F for Female

If you toss a fair coin twice, the sample space are:

S = {HH, TT, HT, TH}
H for Head, T for Tail

Probability Distributions

A probability distribution lists all possible outcomes in the sample space, and the probabilities with which they occur.

It is important to distinguish probability distribution between discrete and continuous random variables.

In the discrete case, one can easily assign a probability to each possible value. For example, when throwing a fair die, each of the six values 1 to 6 has the probability 1/6.

In the continuous random variables, when a random variable takes values from a continuum then, typically, probabilities can be nonzero only if they refer to intervals. For example in quality control one might demand that the probability of a "500 g" package containing between 490 g and 510 g should be no less than 98%.

Complementary Events

Complementary events are two mutually exclusive events whose probabilities add up to 1.

For example:

If a coin is tossed once, the complement of a head is tail.

one toss	head	tail
	50%	50%

If a coin is tossed twice, the complement of outcome head-head is simply the sum of all other three possibilities, tail-tail, head-tail and tail-head.

two tosses	head-head	tail-tail	head-tail	tail-head
	25%	25%	25%	25%