Percentile

When the distribution is normal, Z scores can also be used to calculate Percentiles. Percentile is the percentage of observations that fall below a given data point.

Graphically,percentileis the area below the probability distribution curve to the left of that observation.

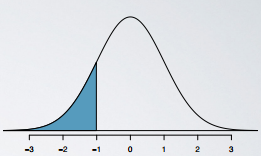
For example, in R, the function pnorm() gives the percentile of an observation, given the mean and the standard deviation of the distribution.

> pnorm(-1, mean = 0, sd = 1)
[1] 0.1586553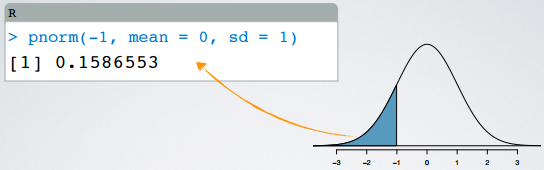

You can also obtain the same probability using a web applet.

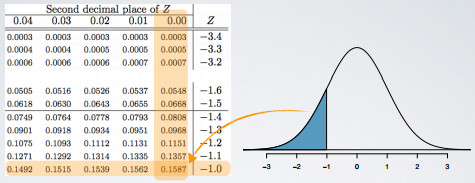
We can also avoid the computation all together and use a Normal Probability Table.

Example 1

Solution 1 - use R pnorm()

> pnorm(1800, mean = 1500, sd = 300)
[1] 0.8413

This means that Pam scored better than 84.13% of the SAT takers.

Solution 2 - use Normal Probability Table

First, we calculate the Z score:

    1800 - 1500
Z = ------------ = 1
       300

Then, in the table, we look for the Z score of 1.

Example 2

We are looking for the cut off value for the top 10% of the distribution. This is a different problem than the Example 1. This time we don't know the value of the observation, but we do know or at least we can get its percentile score.

Since the total area under the curve is 1, the percentile score associated with the cut off value for the top 10% is:

# Work out the percentile score
1 - 0.10 = 0.90

Solution 1: use Z score

The Z score is calculated by:

     observation - mean
Z = ---------------------
             SD

We know the Z, SD, and mean, so the observation can be calculated:

observation = Z * SD + mean

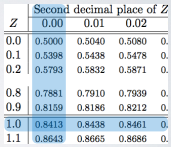
And the Z score can be looked up from Normal Probability Table. Find the closest value, it is 0.8997 in this example.

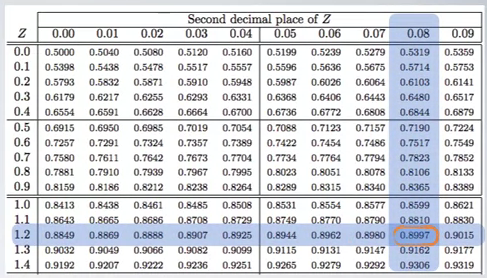
So, it is:

observation = Z * SD + mean = (1.28 × 300) + 1500 = 1844

Solution 2: use R qnorm()

> qnorm(0.90, mean = 1500, sd = 300)
[1] 1884.465

References & Resources

• N/A