Introduction

Calculating probabilities can be hard, often it is hard to figure out what to do . But tree diagrams might be useful to the rescue!

In this section, we will introduce probability trees to solve for conditional probabilities. Highlight that they are especially useful when the probability we are asked for is the reverse of what we are given.

P(A | B) → P(B | A)

The probability tree is introduced through examples.

Probability Tree from Examples

Example 1

The information is organized into a probability tree shown as below:

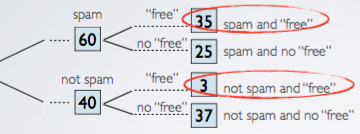
The question is, if an email contains the word "free", what is the probability that it is spam? The email contain word "free" is going to be the given, and we are asked for the probability that is spam. So this is denoted as:

                      35
P(spam | "free") = ---------- = 0.92
                     35 + 3

Example 2

From the study, we know :

• The probability of having HIV is 0.259.

  P(HIV) = 0.259

• The probability of testing positive given HIV is 0.997.

  P(+ | HIV) = 0.997

• The probability of testing negative given no HIV is 0.926.

  P(- | no HIV) = 0.926

In addition, we found the accuracy of the test is dependent on whether the patient has the disease. This conclusion can be explained by:

P(+ | HIV) ≠ P(+ | no HIV)

The question says, if an individual from Swaziland has tested positive, what is the probability that he carries HIV? This question can be denoted as:

P(HIV | +) = ?

                    
                   P(+ | HIV) = 0.997 → P(HIV and +) = P(HIV) × P(+ | HIV) 
                  /                                  = 0.259 × 0.997 = 0.2582
   P(HIV) = 0.259
  /               \
 /                 P(- | HIV) = 0.003 → P(HIV and -) = 0.259 × 0.003 
/                                                    = 0.0008
 
\                   
 \                 P(+ | no HIV) = 0.074 → P(no HIV and +) = 0.741 × 0.074
  \               /                                        = 0.0548
   P(no HIV) = 0.741
                  \
                   P(- | no HIV) = 0.926 → P(no HIV and -) = 0.741 × 0.926
                                                           = 0.6862

So, according to Bayes Theorem, the P(HIV | +) is:

               P(HIV and +)          0.2582
P(HIV | +) = ---------------- = ----------------- = 0.82
                  P(+)           0.2582 + 0.0548

Therefore, there is an 82% chance that individual from Swaziland who has tested positive actually carries HIV.