Standardized score

Definition of Standardized (Z) score

The standardized (Z) score of an observation is the number of standard deviations it falls above or below the mean.

    observation - mean
Z = -------------------
          SD

Note: the Z actually comes from the Z in standardized, which might sound a little odd. The reason not using S, the initial letter of the word, is because we tend to spare S for standard deviations and we don't want to be confusing our abbreviations.

Z score features

Here are some features about Z score:

Z score of mean is zero;
Usually, observation with |Z| > 2 are considered as unusual.

Standardizing with Z scores

Use 68-95-99.7% rule to estimate the standard deviation

A college admissions officer wants to determine which of the two applicants scored better on their standardized test with respect to the other test takers: Pam, who earned an 1800 on her SAT, or Jim, who scored a 24 on his ACT?

SAT score is nearly normally distributed with - N(mean=1500, SD=300)
ACT score is nearly normally distributed with - N(mean=21, SD=5)

We can draw both Pam's and Jim's score:

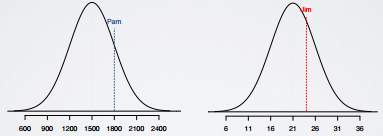
Normal Distribution - z score

We found we can't just compare these raw scores of 1800 vs. 24 since they are measured on different scales. Instead, we want to figure out how many standard deviations above the respected means of their distributions, they scored respectively.

      1800 - 1500
Pam = ------------ = 1
          300
 
       24 - 21
Jim = -------- = 0.6
          5

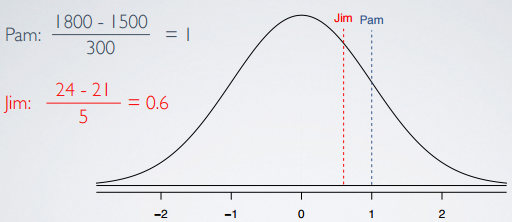
Normal Distribution - z score

So, by ploting these values on the same distribution, we can see that Pam indeed do better than Jim.

These values are called standardized scores.