Introduction

Fuzzy c-means (FCM) is a method of clustering which allows one piece of data to belong to two or more clusters. This method (developed by Dunn in 1973 and improved by Bezdek in 1981) is frequently used in pattern recognition. Straightly speaking, this algorithm works by assigning membership to each data point correspoinding to each cluster center on the basis of distance between the cluster and the data point. More the data is near to the cluster center more is its membership towards the particular cluster center. Clearly, summation of membership of each data point should be equal to one. The algorithm is based on minimization of the following objective function:

,

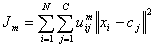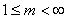
where m (the Fuzziness Exponent) is any real number greater than 1, N is the number of data, C is the number of clusters, u_ij is the degree of membership of x_i in the cluster j, x_i is the ith of d-dimensional measured data, c_j is the d-dimension center of the cluster, and ||*|| is any norm expressing the similarity between any measured data and the center.

Fuzzy partitioning is carried out through an iterative optimization of the objective function shown above, with the update of membership u_ij and the cluster centers c_j by:

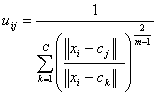
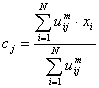
where ||x_i - c_j|| is the Distance from point i to current cluster centre j, ||x_i - c_k|| is the Distance from point i to other cluster centers k.

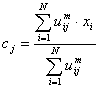
The iteration will stop when 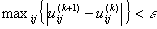, where ε is a termination criterion between 0 and 1, whereas k are the iteration steps. This procedure converges to a local minimum or a saddle point J_m.

The algorithm is composed of the following steps:

Randomly select cluster centre Initialize U=[ uij ] matrix, U(0) Calculate the the uij using: At k-step: calculate the centres vectors C(k)=[cj] with U(k) Update U(k) , U(k+1) If || U(k+1) - U(k)||< ε or the minimum J is achieved, then STOP; otherwise return to step 2.

Parameters of the FCM algorithm

Before using the FCM algorithm, the following parameters must be specified:

• the number of clusters, c,
• the fuzziness exponent, m,
• the termination tolerance, ε.

Advantage and Disadvantage

Advantages:

1. Gives best result for overlapped data set and comparatively better than k-means algorithm.
2. Unlike k-means where data point must exclusively belong to one cluster center here data point is assigned membership to each cluster center as a result of which data point may belong to more than one cluster center.

Disadvantages:

1. Apriori specification of the number of clusters.
2. With lower value of β we get the better result but at the expense of more number of iteration.
3. Euclidean distance measures can unequally weight underlying factors.

Example 1

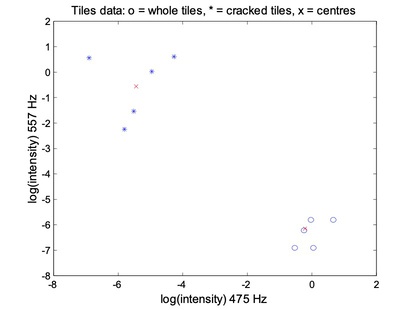
Tiles are made from clay moduled into the right shape, brushed, glazed, and baked. Unfortunately, the baking may produce invisible cracks. Operators can detect the cracks by hitting the tiles with a hammer, and in an automated system the response is recorded with a microphone, filtered, Fourier transformed, and normalised. A small set of data is given in above table.

Plot of tiles by frequencies (logarithms). The whole tiles (o) seem well sparated from the cracked tiles (*). The objective is to find the two clusters.

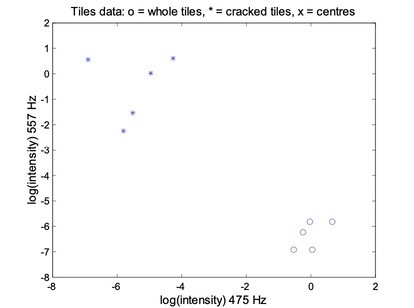
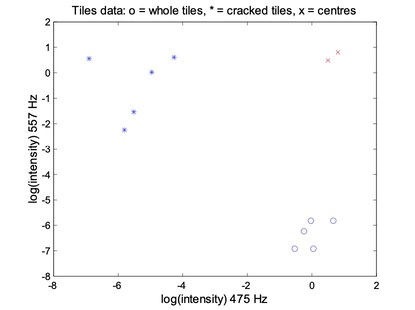
For the FCM, each data point belongs to two clusters to different degrees. Then,

1. Place two cluster centres;
2. Assign a fuzzy membership to each data point depending on distance;

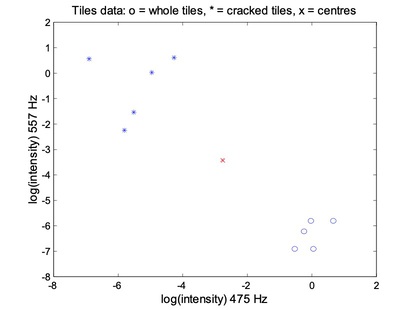
1. Computer the new centre of each class;
2. Move the crosses (x)

Iteration 2

Iteration 5

Iteration 10

Iteration 13 (then stop, because no visible change). Each data point belongs to the two clusters to a degree.

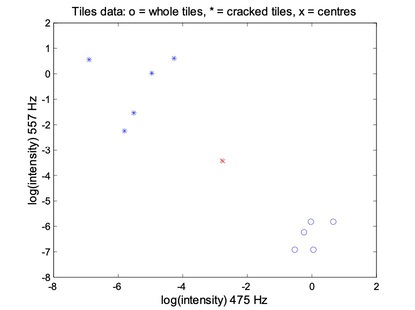
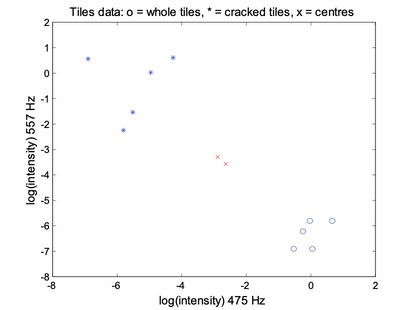
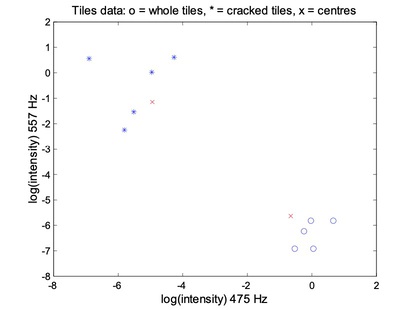
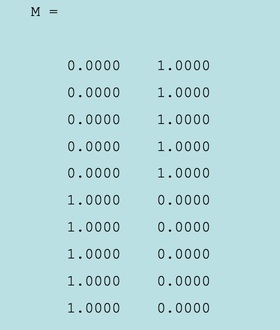
The membership matrix M:

1. The last five data points (rows) belong mostly to the first cluster;
2. The frist five data points (rows) belong mostly to the second cluster;

References & Resources

• http://home.dei.polimi.it/matteucc/Clustering/tutorial_html/cmeans.html
• http://homes.dsi.unimi.it/~valenti/SlideCorsi/Bioinformatica05/Fuzzy-Clustering-lecture-Babuska.pdf
• https://sites.google.com/site/dataclusteringalgorithms/fuzzy-c-means-clustering-algorithm