Introduction

Now, we look at our first implementation of an algorithm for solving the dynamic connectivity problem, called Quick-find. This is a so called eager algorithm, for solving kind activity problem.

Quick-find Data Structure

The data structure that we are going to use to support the algorithm is simply an integer array indexed by object. The interpretation is the two objects, P and Q are connected if and only if their entries in the array are the same.

• Integer array id[] of length N
• Interpretation: P and Q are connected if they have the same id.

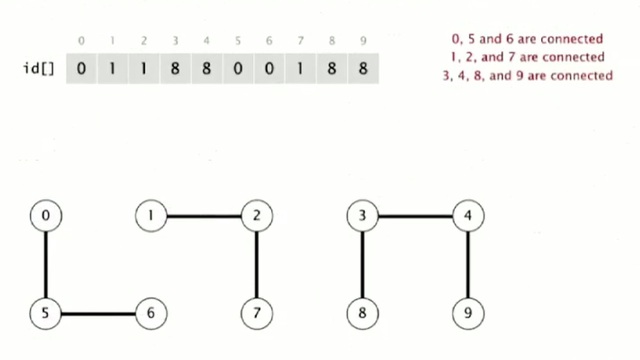
So for example in this example with our ten objects the idea array that describes the situation after seven connections is illustrated in the figure below.

• Find operation: check if p and q have the same id
  
• Union operation: to merge components containing p and q, change all entries whose id equals id[p] to id[q]
  

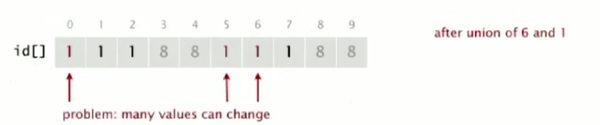
So that, after the, at this point 0, 5, and 6 are all in the same connected component, because they have the same array entry, zero. 1, 2, and 7 all have entry one. And 3, 4, 8, and 9 all have entry eight. So that representation is, shows that they're connected. And clearly, that's going to support a quick implementation of the find operation. We just check the array entries to see if they're equal. Check if P and Q have the same ID. So, 6 and 1 have different IDs. 1 has ID one, 6 has ID zero. They're not in the same connected component. Union is more difficult in order to merge the components, containing two given objects. We have to change all the entries, whose ID is equal to one of them to the other one. And arbitrarily we choose to change the ones that are the same as P to the ones that are same as Q. So if we're going to union 6 and 1, then we have to change entries 0, 5, and 6. Everybody in the same connected component as 6. From zero to one. And this is, as we'll see, this is a bit of a problem when we have a huge number of objects, because there's a lot of values that can change. But still, it's easy to implement.

Quick-find: Java implementation

Quick-find efficiency (It is too slow)

Now we need to decide how effective or efficient that Quick-find algorithm is going to be. In this example, we only think about the number of times the code has to access the array.

Cost model: number of array access (for read and write)

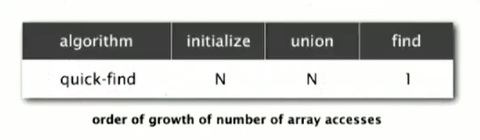
As we saw, when doing the implementation, both the initialized and union operations involved the for-loop that go through the entire array. So they have to touch in a constant proportional to N times after touching array entry. Find operation is quick, it is just to a constant number of times check array entries.

Quick-find defect: Union is too expensive, it take N² array access to process a sequence of N union commands on N objects. This is a typical quadratic time which we always need to avoid.

Reason to avoid quadratic algorithms

The quadratic time is too slow and we can't accept quadratic time algorithm for large problems. The reason is they don't scale.

As computers get faster, quadratic algorithms actually get slower. A very rough standard, say for now, is that people have computers that can run billions of operations per second, and they have billions of entries in main memory. So, that means that you could touch everything in the main memory in about a second. That's kind of an amazing fact that this rough standard is really held for 50 or 60 years. The computers get bigger but they get faster so to touch everything in the memory is going to take a few seconds.

Now it's true when computers only have a few thousand words of memory and it's true now that they have billions or more. So let's accept that as what computers are like. Now, that means is that, with that huge memory, we can address huge problems. So we could have, billions of objects, and hope to do billions of union commands on them. And, but the problem with that quick find algorithm is that, that would take 10^18th operations, or, say array axises or touching memory. And if you do the math, that works out to 30 some years of computer time. Obviously, not practical to address such a problem on today's computer.

And the reason is, and the problem is that quadratic algorithms don't scale with technology. You might have a new computer that's ten times as fast but you could address a problem that's ten times as big. And with a quadratic algorithm when you do that. It's going to be ten times as slow. That's the kind of situation we're going to try to avoid by developing more efficient algorithms for solving problems like this.

References & Resources

• N/A