Linguistic Variables

In practice, when the universe of discourse X is a continuous space ( the real line R or its subset ), we usually partition X into several fuzzy sets whose MFs cover X in a more or less uniform manner. These fuzzy sets, which usually carry names that conform to adjectives appearing in our daily linguistic usage, such as "large", "medium" or "small" are called linguistic values or linguistic labels. Thus, the universe of discourse X is often called linguistic variable. Here is a simple example.

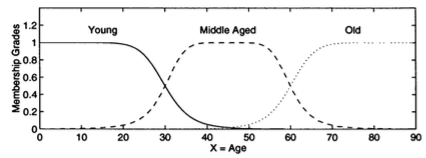
Linguistic variables and linguistic values

Suppose that X = "age". Then we can define fuzzy sets "young", "middle aged" and "old" that are characterized by MFs μ_young(x), μ_middleaged(x) and μ_old(x), respectively. Just as variable can assume various values, a linguistic variable "Age" can assume different linguistic values, such as "young", "middle aged" and "old" in this case. If "age" assumes the value of "young", then we have the expression "age is young", and so forth for the other values. Typical MFs for these linguistic values are displayed in the figure below, where the universe of discourse X is totally covered by the MFs and the transition from one MF to another is smooth and gradual.

A fuzzy set is unique specified by its membership function. To describe membership functions more specifically, the nomenclature are used in the literature.

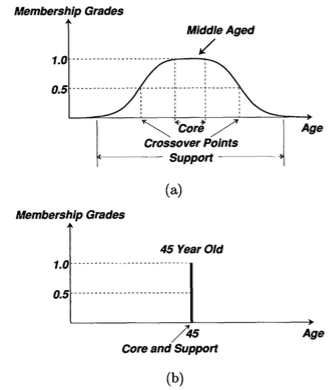
Support

The support of a fuzzy set A is the set of all points x in X such that μ_A(x) > 0:

support(A) = { x | μA(x) > 0 }

Core

The core of a fuzzy set A is the set of all points x in X such that μ_A(x) > 1:

core(A) = { x | μA(x) = 1 }

Normality

A fuzzy set A is normal if its core is nonempty. In other words, we can always find a points x ∈ X such that μ_A(x) = 1

Crossover points

A crossover point of a fuzzy set A is a point x ∈ X at which μ_A(x) = 0.5

crossover(A) = { x | μA(x) = 0.5 }

Fuzzy singleton

A fuzzy set whose support is single point in X with x μ_A(x) = 1 is called a fuzzy singleton.

Figure below illustrate the cores, supports and crossover points of the bell-shaped membership function representing "middle aged" and of the fuzzy singleton characterizing "45 years old".

α-cut and strong α-cut

The α-cut or α-level set of a fuzzy set A is a crisp set defined by

Aα = { x | μA(x) ≥ α }

Strong α-cut or strong α-level set are defined similarly:

Aα' = { x | μA(x) > α }

Using the notation for a level set, we can express the support and core of a fuzzy set A as

support(A) = A0'

and

core(A) = A1

respectively.

Convexity

A fuzzy set A is convex if and only if for any x₁, x₂ ∈ X and any λ ∈ [0, 1],

μA(λx1 + (1 - λ)x2) ≥ min{ μA(x1), μA(x2) }

Alternatively, A is convex if all its α-level sets are convex.

A crisp set C in Rⁿ is convex if and only if for any two points x₁ ∈ C and x₂ ∈ C, their convex combination λx₁ + ( 1 - λ)x₂ is still in C, where 0 ≤ λ ≤ 1. Hence the convexity of a (crisp) level set A_α implies that A_α is composed of a single line segment only.

Note that the definition of convexity of a fuzzy set is not as strict as the common definition of convexity of a function. For comparison, the definition of convexity of a function f(x) is

f( λx1 + ( 1 - λ )x2 ) ≥ λf(x1) + ( 1 - λ )f(x2)

which has a tigher condition.

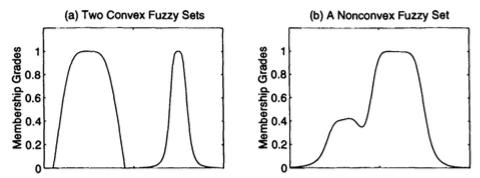
Figure below illustrates the concept of convexity of fuzzy sets; Figure (a) shows two convex fuzzy sets, the left fuzzy set satisfies both Equations, while the right one satisfies Equation 1 only. Figure (b) is a nonconvex fuzzy set.

Fuzzy numbers

A fuzzy number A is a fuzzy set in the real line (R) that satisfies the conditions for normality and convexity.

Most (noncomposite) fuzzy sets used in the literature satisfy the conditions for normality and convexity, so fuzzy numbers are the most basic type of fuzzy sets.

Bandwidths of normal and convex fuzzy sets

For a normal and convex fuzzy set, the bandwidths or width is defined as the distance between the two unique crossover points:

width(A) = | x2 - x1 |

where μ_A(x₁) = μ_A(x₂) = 0.5.

Symmetry

A fuzzy set A is symmetric if its MFs is symmetric around a certain point x = c, namely,

μA( c + x ) = μA( c - x ) for all x ∈ X 

Open left, open right, closed

A fuzzy set A is

• open left if

  limx→-∞μA(x) = 1 and limx→+∞μA(x) = 0; 

• open right if

  limx→-∞μA(x) = 0 and limx→+∞μA(x) = 1;  

• closed if

  limx→-∞μA(x) = limx→+∞μA(x) = 0;

For example, the fuzzy set "young" is open left; "old" is open right; and "middle aged" is closed.