Introduction

The correlation is one of the most common and most useful statistics. A correlation is a single number that describes the degree of relationship between two variables. Let’s work through an example to show how this statistics is computed.

Correlation Example

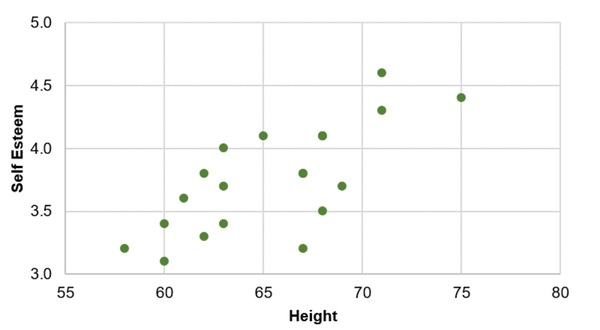
Let’s assume that we want to look at the relationship between two variables, height and self esteem. Perhaps we have a hypothesis that how tall you affect your self esteem. Let’s say we collect some data from 20 individuals. Height is measured in inches. Self esteem is measured based on the average of 10 1-to-5 rating items, where higher scores mean higher self esteem. Below is the data:

Person	Height	Self Esteem
1	68	4.1
2	71	4.6
3	62	3.8
4	75	4.4
5	58	3.2
6	60	3.1
7	67	3.8
8	68	4.1
9	71	4.3
10	69	3.7
11	68	3.5
12	67	3.2
13	63	3.7
14	62	3.3
15	60	3.4
16	63	4.0
17	65	4.1
18	67	3.8
19	63	3.4
20	61	3.6

Now, let’s take a quick look at the histogram for each variable:

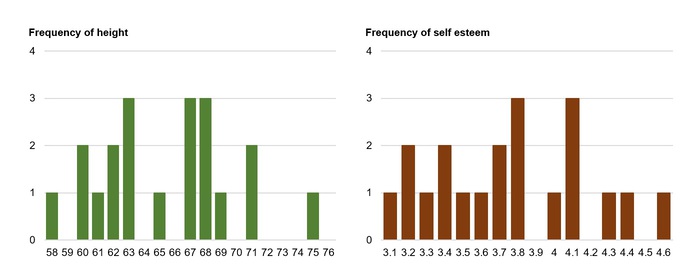
And, here are the descriptive statistics:

Variable	Mean	StDev	Variance	Sum	Minimum	Maximum	Range
Height	65.4	4.40574	19.4105	1308	58	75	17
Self Esteem	3.755	0.426090	0.181553	75.1	3.1	4.6	1.5

Finally, we’ll look at the simple bi-variate plot:

Calculating the Correlation

Now we are ready to compute the correlation value. The formula for the correlation is:

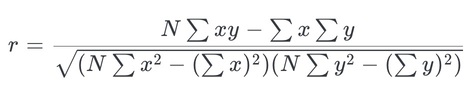
Where N is the number of the pair, ∑xy is the sum of the products of the pair, ∑x is the sum of x, ∑y is the sum of y, ∑x² is the sum of the squared x, ∑y² is the sum of the squared y.

For above case, N=20, ∑xy=4937.6, ∑x=1308, ∑y=75.1, ∑x² =85912, ∑y²=285.45. Now, when we plug these values into the formula given above, we get the following:

The correlation for this case is 0.73, which is a fairly strong positive relationship. So, we guess there is a relationship between height and self esteem, at least in this made up data!

References & Resources

• N/A