Data Have Short Tails

The following is a normal probability plot for 500 random numbers generated from a Tukey-Lambda distribution with the λ parameter equal to 1.1.

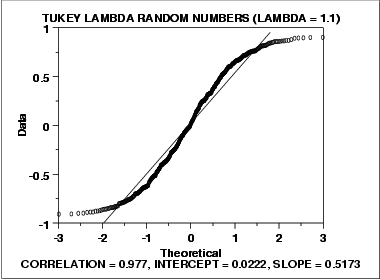
We can make the following conclusions from the above plot.

1. The normal probability plot shows a non-linear pattern.
2. The normal distribution is not a good model for these data.

For data with short tails relative to the normal distribution, the non-linearity of the normal probability plot shows up in two ways. First, the middle of the data shows an S-like pattern. This is common for both short and long tails. Second, the first few and the last few points show a marked departure from the reference fitted line. In comparing this plot to the long tail example in the next section, the important difference is the direction of the departure from the fitted line for the first few and last few points. For short tails, the first few points show increasing departure from the fitted line above the line and last few points show increasing departure from the fitted line below the line. For long tails, this pattern is reversed.

In this case, we can reasonably conclude that the normal distribution does not provide an adequate fit for this data set. For probability plots that indicate short-tailed distributions, the next step might be to generate a Tukey Lambda PPCC plot. The Tukey Lambda PPCC plot can often be helpful in identifying an appropriate distributional family.

References & Resources

• N/A