Introduction

The Fibonacci numbers or Fibonacci sequence are the numbers in the following integer sequence:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ...
 
or (often, in modern usage)
 
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ...

Definition

By definition, the first two numbers in the Fibonacci sequence are either 1 and 1, or 0 and 1, depending on the chosen starting point of the sequence, and each subsequent number is the sum of the previous two.

• The 2 is found by adding the two numbers before it (1+1)
• Similarly, the 3 is found by adding the two numbers before it (1+2),
• And the 5 is (2+3),
• and so on ...

In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation.

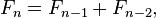
with seed values:

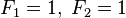
or

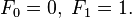
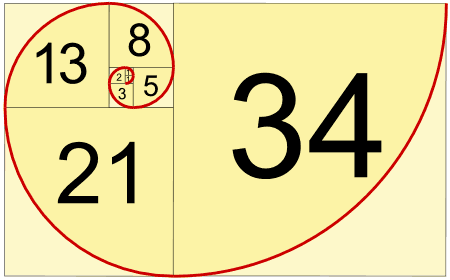
Makes a Spiral

When we make squares with those widths, we get a nice spiral:

Golden Ratio

And here is a surprise. When we take any two successive (one after the other) Fibonacci Numbers, their ratio is very close to the Golden Ratio "φ" which is approximately 1.618034...

In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:

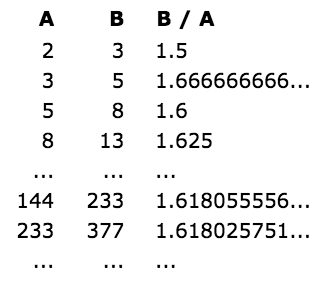
Note: this also works when we pick two random whole numbers to begin the sequence, such as 192 and 16 (we get the sequence 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, ...):

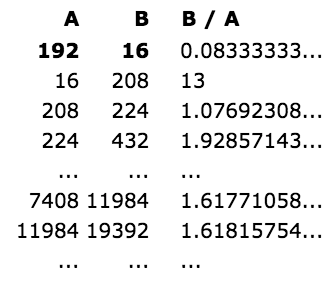
It takes longer to get good values, but it shows that not just the Fibonacci Sequence can do this.

Using the Golden Ratio to Calculate Fibonacci Numbers

And even more surprising is that we can calculate any Fibonacci Number using the Golden Ratio:

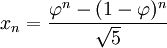
The answer always comes out as a whole number, exactly equal to the addition of the previous two terms.

Example: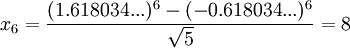

A Pattern

Here is the Fibonacci numbers again:

n =	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	...
xn =	0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	...

There is an interesting pattern:

• Look at the number x3 = 2. Every 3rd number is a multiple of 2 (2, 8, 34, 144, 610, ...)
• Look at the number x4 = 3. Every 4th number is a multiple of 3 (3, 21, 144, ...)
• Look at the number x5 = 5. Every 5th number is a multiple of 5 (5, 55, 610, ...)
• every nth number is a multiple of x_n

Value below Zero

In fact the sequence below zero has the same numbers as the sequence above zero, except they follow a +-+- ... pattern.

n =	...	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	...
xn =	...	-8	5	-3	2	-1	1	0	1	1	2	3	5	8	...