Introduction

In mathematics, the geometrix mean is a type of mean or average, which indicates the central tendency or typical value of a set of numbers by using the product of their values (as oppose to the arithmetic mean which uses their sum). The geometric mean is defined as the nth root (where n is the count of numbers) of the product of the numbers.

For instance, the geometric mean of two numbers, say 2 and 8, is just the square root of their product; that is sqrt(2*8) = 4. As another example, the geometric mean of the three numbers 4, 1, and 1/32 is the cube root of their product (1/8), which is 1/2; that is .

A geometric mean is often used when comparing different items - finding a single "figure of merit" for these items - when each item has multiple properties that have different numeric ranges.

The geometric mean can be understood in terms of geometry, as shown in Figure below. The geometric mean of two numbers, a and b, is the length of one side of a square whose area is equal to the area of a rectangle with sides of lengths a and b. Similarly, the geometric mean of three numbers, a, b, and c, is the length of one side of a cube whose volume is the same as that of a cuboid with sides whose lengths are equal to the three given numbers.

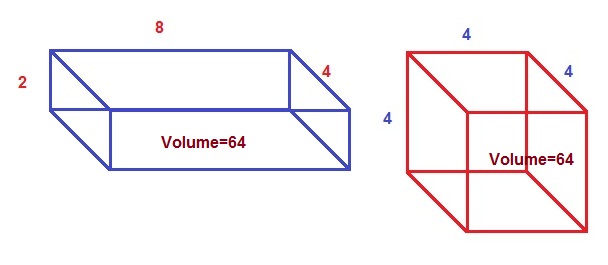
The geometric mean applies only to positive numbers. It is also often used for a set of numbers whose values are meant to be multiplied together or are exponential in nature, such as data on the growth of the human population or interest rate of a financial investment.

Calculation

The geometric mean of a data set {a₁, a₂, ..., a_n} is given by:

The geometric mean of a data set is less than the data set's arithmetic mean unless all members of the data set are equal, in which case the geometric and arithmetic means are equal. This allows the definition of the arithmetic-geometric mean, a mixture of the two which always lies in between.

Applications

Proportional growth

The geometric mean is more appropriate than the arithmetic mean for describing proportional growth, both exponential growth (constant proportional growth) and varying growth; in business the geometric mean of growth rates is known as the compoundannual growth rate (CAGR). The geometric mean of growth over periods yields the equivalent constant growth rate that would yield the same final amount.

Suppose an orange tree yields 100 oranges one year and then 180, 210 and 300 the following years, so the growth is 80%, 16.6666% and 42.8571% for each year respectively. Using the arithmetic mean calculates a (linear) average growth of 46.5079% (80% + 16.6666% + 42.8571% divided by 3). However, if we start with 100 oranges and let it grow 46.5079% each year, the result is 314 oranges, not 300, so the linear average over-states the year-on-year growth.

Instead, we can use the geometric mean. Growing with 80% corresponds to multiplying with 1.80, so we take the geometric mean of 1.80, 1.166666 and 1.428571, i.e. ; thus the "average" growth per year is 44.2249%. If we start with 100 oranges and let the number grow with 44.2249% each year, the result is 300 oranges.

Other applications, please check the Wikipedia.

References & Resources

• https://en.wikipedia.org/wiki/Geometric_mean