Introduction

In probability theory, a probability density function (pdf) (Also known as Probability Distribution Function or Probability Function), or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the integral of this variable’s density over the region. The probability density function is nonnegative everywhere, and its integral over the entire space is equal to one.

The terms Probability Distribution function or Probability Function have also sometimes been used to denote the PDF. However, this use is not standard among probability and statisticians. In other sources, Probability Distribution function may be used when the probability distribution is defined as a function over general sets of values, or it may refer to the cumulative distribution function.

Absolutely Continuous Univariate Distributions

A probability density function is most commonly associated with absolutely continuous univariate distributions. A random variable X has density f, where f is non-negative Lebesgue-integrable function, if:

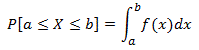
Hence, if F is the cumulative distribution function of X, then:

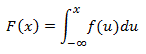
And:

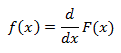
Intuitively, one can think of f(x)dx as being the probability of X falling within the infinitesimal interval [x, x+dx].

References & Resources

• N/A