Introduction

The Binomial Distribution describes the probability of having exactly k successes in n independent Yes/No (success/failure) experiment with probability of success p. The Yes/No (success/failure) experiment is also called a Bernoulli experiment or Bernoulli trial.

Binomial probability can be calculated as

Binomial probability = number of scenarios × P(single scenario)

The probability of single scenario, P(single scenario), is simply

P(single scenario) = pk(1 - p)(n - k)
 
pk means the probability of success to the power of number of successes. 
(1 - p)(n - k) means the probability of failure to the power of number of failures. 

If there were many more, say we are looking for how many scenarios for 4 success in 100 trials, above method would be very tedious, and very error prone. Therefore, we usually use an alternative approach, namely the choose function which is useful for calculating the number of ways to choose k successes in n trials.

To evaluate this choose function, we divide n factorial by k factorial times n-k factorial.

Choose function - examples

n = 4, k = 1
             4!          4 × 3 × 2 × 1
(4 1) = ------------- = ---------------- = 4
         1! × (4-1)!     1 × 3 × 2 × 1

In R, the associate function is also called choose and it takes two arguments n and k. So:

> choose(4,1)
[1] 4

n = 9, k = 2
             9!          9 × 8 × 7!
(9 2) = ------------- = ------------- = 36
         2! × (9-2)!     2 × 1 × 7! 

In R, the associate function is also called choose and it takes two arguments n and k. So:

> choose(9,2)
[1] 36

Definition of Binomial Distribution

Put all above together, if p represents probability of success, (1-p) represents probability of failure, n represents number of independent trials, and k represents number of success:

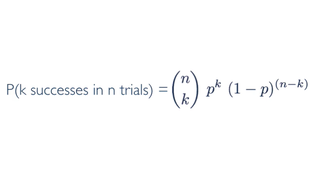
where:

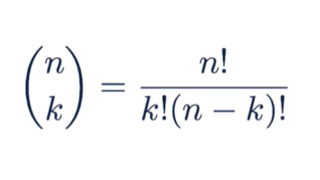
Binomial Conditions

What does it take for a random variable to follow a binomial distribution? Here are the 4 conditions:

1. The trials must be independent.
2. The number of trials, n , must be fixed.
3. Each trial outcome must be classified as a success or a failure.
4. The probability of success, p, must be the same for each trial.

Examples 1

We can find this probability answer using the binomial distribution, because it actually meet the conditions required for the binomial distribution.

Solution 1 - Calculate by hand

n = 10
p = 0.13
1 - p = 0.87
k = 8
 
Therefore, 
P(k = 8) = (10  8) × 0.138 × 0.872
 
      10!         
= ----------  × 0.138 × 0.872
   8! × 2!
 
= 0.00000278

Solution 2 - Use R dbinom()

We can also calculate the same probability using R, dbinom() and takes 3 arguments. The 1st argument is the number of successes, the 2nd argument is sample size or the number of trials, and the 3rd argument is the probability of success.

> dbinom(8, size = 10, p = 0.13)
[1] 2.77842e-06

Solution 3 - Use web app

The app link is available from https://gallery.shinyapps.io/dist_calc/

References & Resources

• N/A