Introduction

In this section, we are going to work with confidence intervals. Specifically, we are going to learn how to calculate the required sample size to achieve a certain margin of error.

We are also going to discuss sample size vs. accuracy.

Given a target margin of error, confidence level, and information on the variability of the sample (or population), we can determine the required sample size to achieve the desired margin of error.

We do this by plugging known values into the equation of the margin of error and then rearranging things to solve for the unknown sample size:

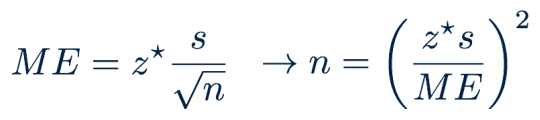
Example

So, we know:

• The desired margin of error is ≤ 4, ME ≤ 4 ;
• The confidence level we are going to use is 90%, CL = 90% ;
• The critical value assiciated with 90% confidence level is 1.65, z^* = 1.65 ;
• The SD of IQ scores of these children is going to be 18, σ = 18 ;

The next is to plug everything that we know into the equation:

          18             1.65 × 18
4 = 1.65 ---- , so n = ( ---------- ) 2 = 55.13
          √n                 4

However, since we can't have a .13 of a person, so we need to round this number to nearest big integer, that is 56. So we need at least 56 such children in the sample to obtain a maximum margin of error.

We can certainly do this by solving directly for n again, but we can actually also make use of our solution from earlier.

The previous desired margin error was 4 and the new desired margin of error is 2 points. Therefore, we can multiple both side by 1/2.

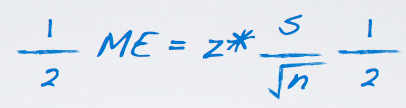
This is equivalent to multiplying the sample size by 4 actually, since the sample size is in denominator and under the square root sign.

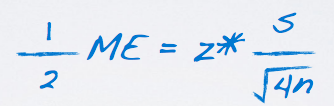
Therefore, we see if they want better results or more accurate results that they should increase sample size. However, you may need to really, really increase your sample size, for example it is 224 in this case.

References & Resources

• N/A