Introduction

A confusion matrix (Kohavi and Provost, 1998) contains information about actual and predicted classifications done by a classification system. Performance of such systems is commonly evaluated using the data in the matrix. The following table shows the confusion matrix for a two class classifier.

The entries in the confusion matrix have the following meaning in the context of our study:

• a is the number of correct predictions that an instance is negative;
• b is the number of incorrect predictions that an instance is positive;
• c is the number of incorrect predictions that an instance is negative;
• d is the number of correct predictions that an instance is positive;

		Predicted
		Negative	Positive
Actual	Negative	a	b
	Positive	c	d

Several standard terms have been defined for the 2 class matrix:

1) The accuracy (AC)is the proportion of the total number of predictions that were correct. It is determined using the equation:

(1)

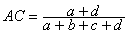
2) The recall or true positive rate (TP or TPR) is the proportion of positive cases that were correctly identified, as calculated using the equation:

(2)

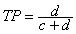
3) The false positive rate (FP or FPR) is the proportion of negatives cases that were incorrectly classified as positive, as calculated usingthe equation :

(3)

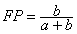
4) The true negative rate (TN or TNR) is defined as the proportion of negatives cases that were classified correctly, as calculated using the equation:

(4)

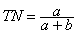
5) The false negative rate (FN or FNR) is the proportion of positives cases that were incorrectly classified as negative, as calculated using the equation:

(5)

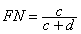
6) Finally, precision (P) is the proportion of the predicted positive cases that were correct, as calculated using the equation:

(6)

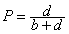
The accuracy determined using equation 1 may not be an adequate performance measure when the number of negative cases is much greater than the number of positive cases (Kubat et al., 1998). Suppose there are 1000 cases, 995 of which are negative cases and 5 of which are positive cases. If the system classifies them all as negative, the accuracy would be 99.5%, even though the classifier missed all positive cases. Other performance measures account for this by including TP in a product: for example, geometric mean (g-mean) (Kubat et al., 1998), as defined in equations 7 and 8, and F-Measure (Lewis and Gale, 1994), as defined in equation 9:

(7)

(8)

(9)

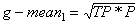
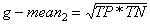
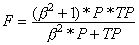
In equation 9, b has a value from 0 to infinity and is used to control the weight assigned to TP and P. Any classifier evaluated using equations 7, 8 or 9 will have a measure value of 0, if all positive cases are classified incorrectly.

Example

If a classification system has been trained to distinguish between cats, dogs and rabbits, a confusion matrix will summarize the results of testing the algorithm for further inspection. Assuming a sample of 27 animals — 8 cats, 6 dogs, and 13 rabbits, the resulting confusion matrix could look like the table below:

		Predicted
		Cat	Dog	Rabbit
Actual	Cat	5	3	0
	Dog	2	3	1
	Rabbit	0	2	11

In this confusion matrix, of the 8 actual cats, the system predicted that three were dogs, and of the six dogs, it predicted that one was a rabbit and two were cats. We can see from the matrix that the system in question has trouble distinguishing between cats and dogs, but can make the distinction between rabbits and other types of animals pretty well. All correct guesses are located in the diagonal of the table, so it's easy to visually inspect the table for errors, as they will be represented by any non-zero values outside the diagonal.

References & Resources

• Wikipedia, http://en.wikipedia.org/wiki/Confusion_matrix
• http://www2.cs.uregina.ca/~dbd/cs831/notes/confusion_matrix/confusion_matrix.html