Introduction

k-Means algorithm was developed by J. MacQueen (1967) and then by J.A. Hartigan and M.A. Wong around 1975. Simply speaking k-means clustering because it is an algorithm to classify or to group your data based on attributes/features into K number of group. K is positive integer number. The grouping is done by minimizing the sum of squares of distances between data and the corresponding cluster centroid (For example: Euclidean distance).

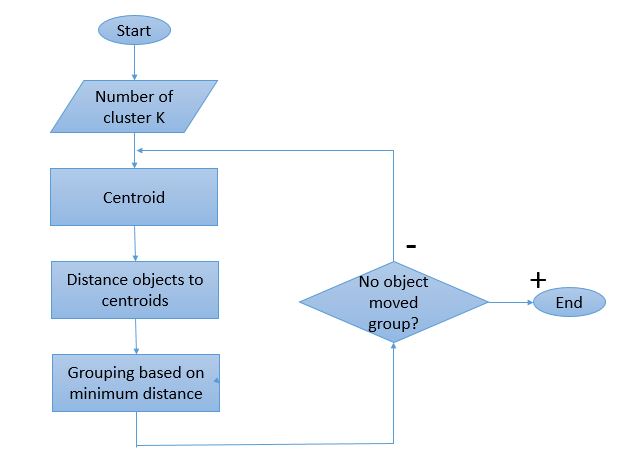
The algorithm is composed of the following steps:

Place K points into the space represented by the objects that are being clustered. Assign each object to the group that has the closest centroid. When all objects have been assigned, recalculate the positions of the K centroids. where n is the number of objects that has the closest centroid to cluster Km Repeat Step 2 and 3 until the centroids no longer move. This produces a separation of the objects into groups from which the metric to be minimized can be calculated.

Example

Use k-Means and Euclidean Distance to cluster the following 8 samples into 3 clusters:

A1=(2,10), A2=(2,5), A3=(8,4), A4=(5,8), A5=(7,5), A6=(6,4), A7=(1,2), A8=(4,9)

Figure 1: (a) 8 samples (b) 3 clusters (seed1, seed2 and seed3) in red

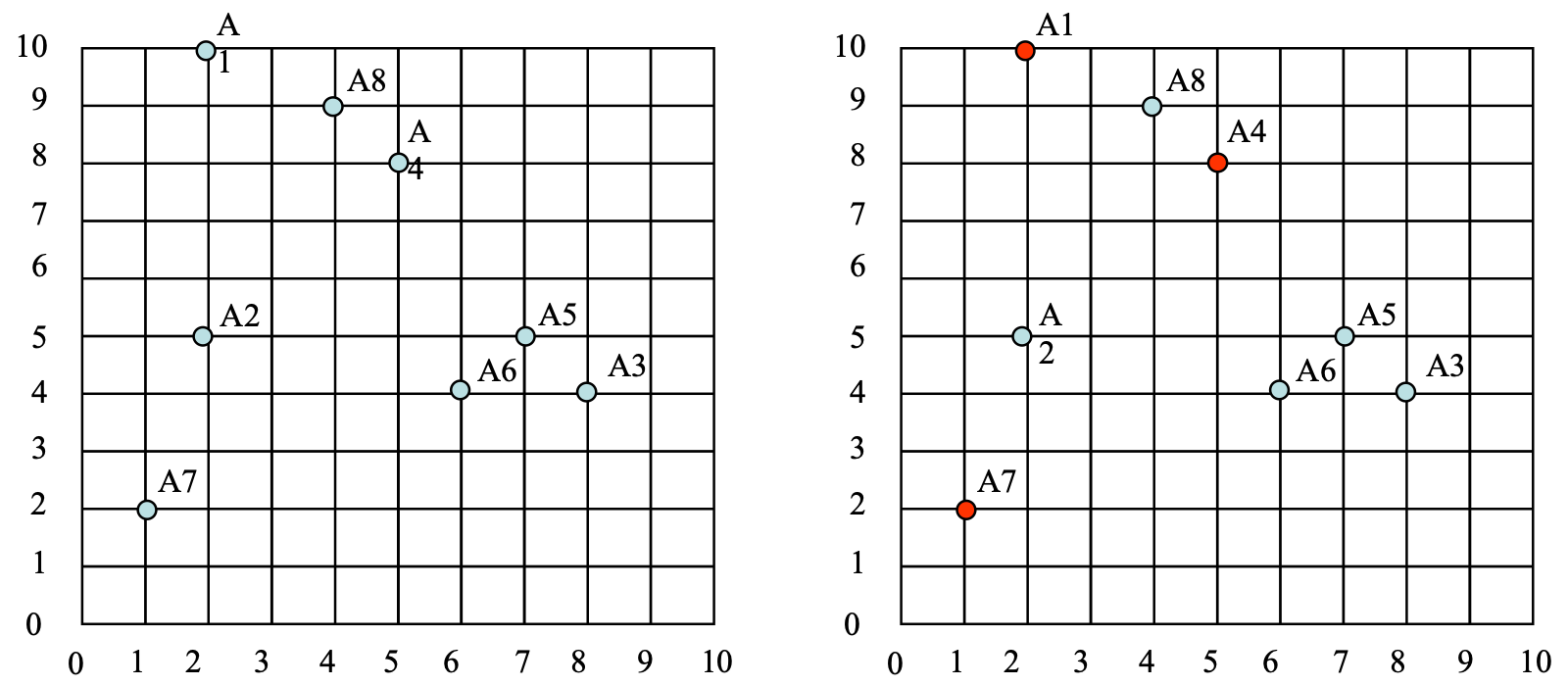
At the beginning, we initial the centre of the 3 clusters (seed1, seed2 and seed3) to A1, A4 and A7 (Figure 1 (b)).

Then, Epoch 1

Figure 2: (a) before Epoch 1; (b) centroid has been changed after Epoch 1

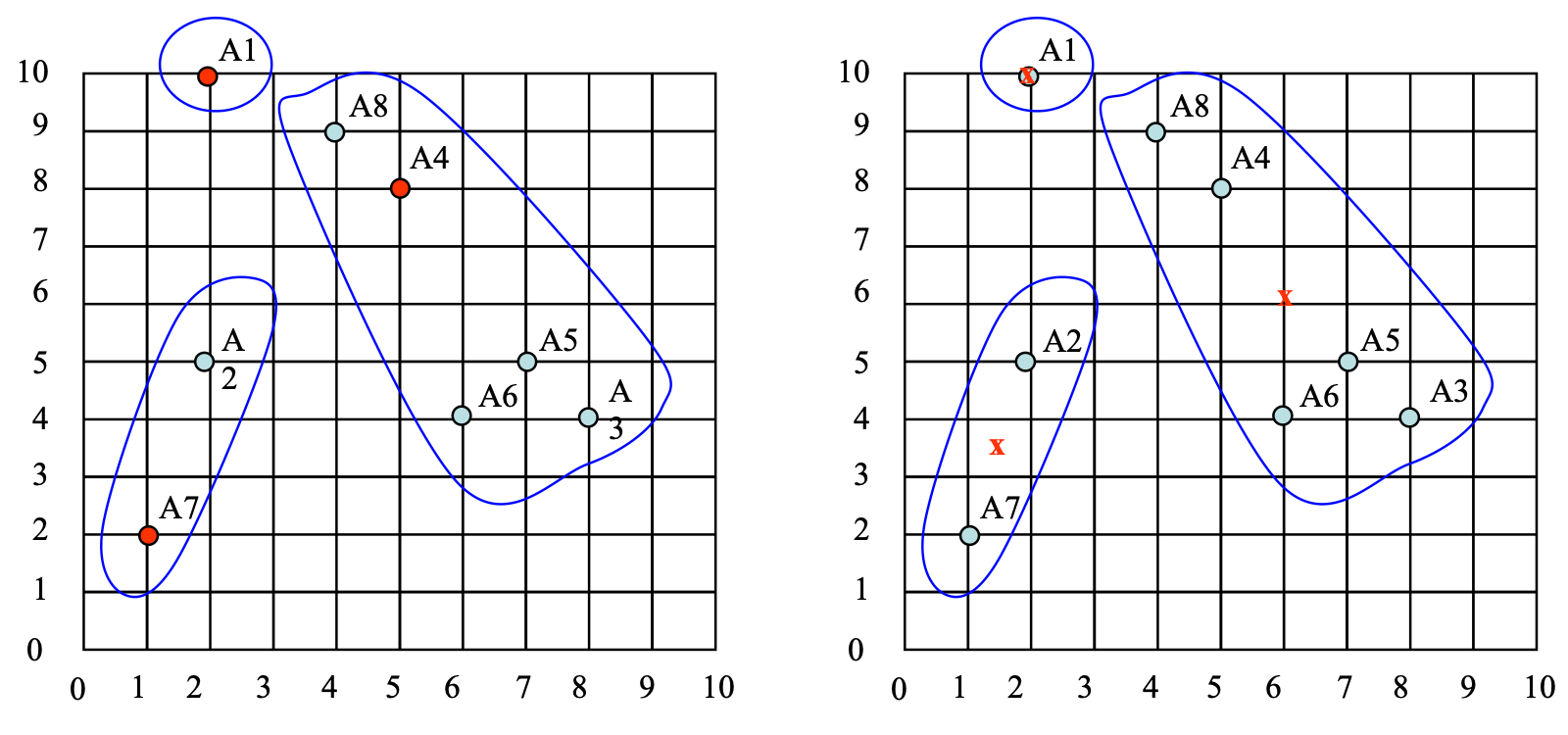
Epoch 2 (Omit), after the 2nd epoch the results would be:

1: {A1, A8}, 2: {A3, A4, A5, A6}, 3: {A2, A7} with centres C1= (3, 9.5), C2= (6.5, 5.25) and C3= (1.5, 3.5)

Epoch 3 (Omit), after the 3rd epoch the results would be:

1: {A1, A4, A8}, 2: {A3, A5, A6}, 3: {A2, A7} with centre C1= (3.66, 9), C2= (7, 4.33) and C3= (1.5, 3.5)

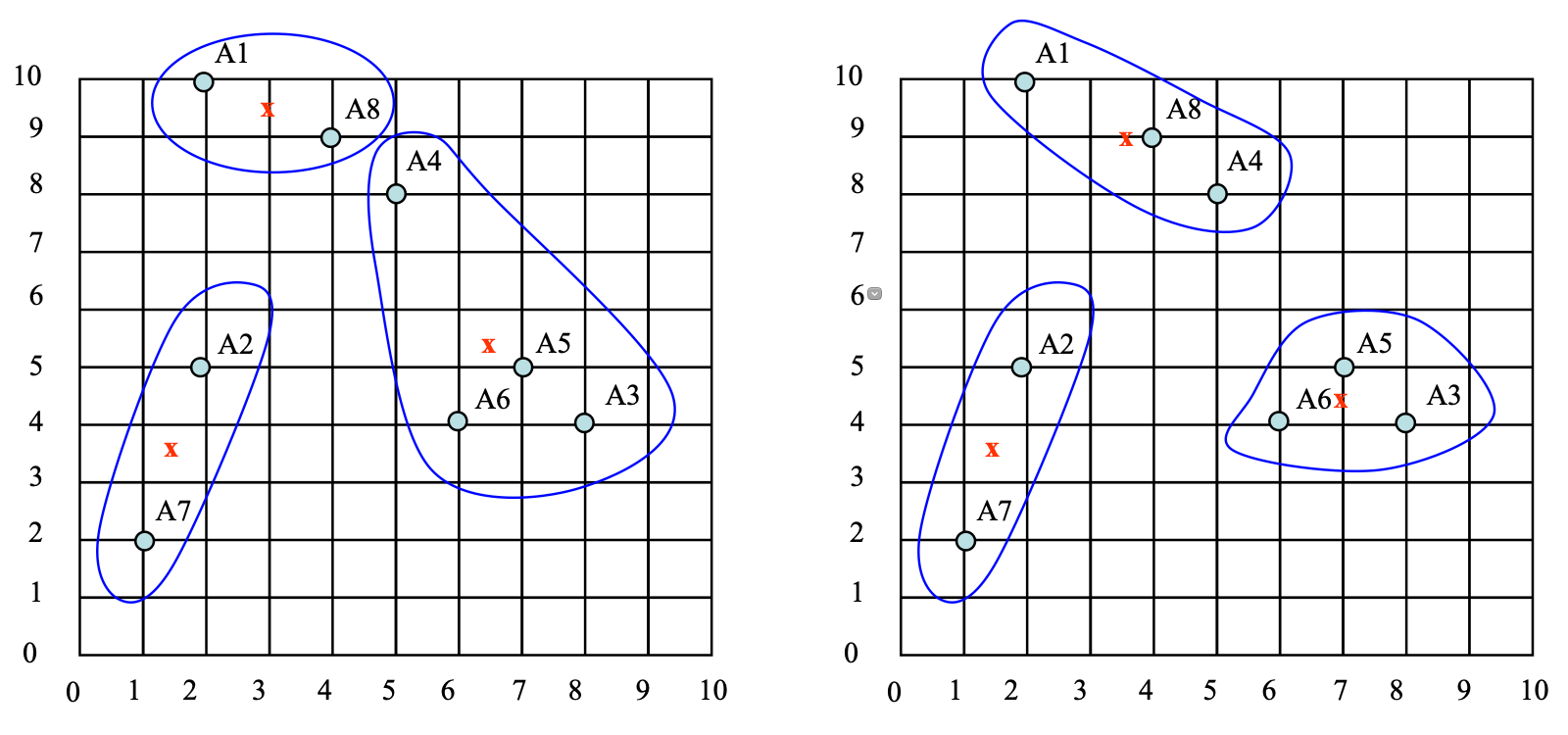
After Epoch 3, the centroids no longer move. So, the clustering is finish.

References & Resources

• N/A