Dynamic connectivity problem

Now, we talk about the dynamic connectivity problem, the model of the problem for union find. Here is the idea. They are going to have a set of N objects. Doesn't really matter what they are, we use the numbers, 0 through N to model our objects. And then, we have the idea of a connection between two objects. And, we postulate that there is a command that says, connect two objects. Given two objects, provide a connection between them. And then key part of the problem is find query or the connected query, which just asks, is there a path connecting the two objects.

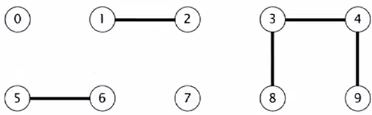
For example, in this set of 10 objects, we performed already, a bunch of union commands, connecting (4 and 3), (3 and 8), (6 and 5), ( 9 and 4), (2 and 1). And now we might have aconnected query that says, is 0 connected to 7? In this case, there is no connection, so we say no. But if we ask is 8 connected to 9? We are going to say yes, even there is no direct connection between 8 and 9. There is a path from 8 to 3 to 4 to 9.

So, that's our problem, to be able to officially support these two commands for given set of objects.

• Union command: connect two objects
• Find/connected query: is there a path connecting the two objects?

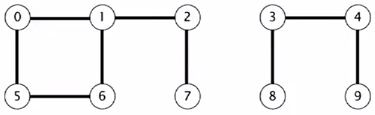
Now, let's say we add union(5,0), union(7,2), union(6,1). So, now if we ask our 0 connected to 7, we are going to answer yes. So that's our problem, intermix union commands and connected queries and we need to be able to officially support those commands for a large number of objects.

Connectivity example

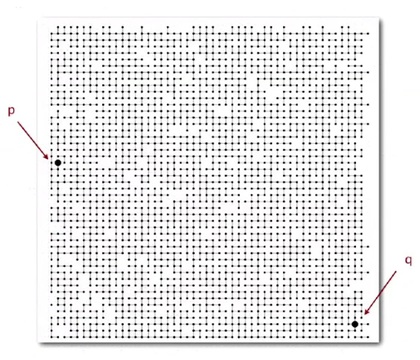
Here is a much bigger example. We would like to ask is that is there any path between p and q? You can see that we are going to need efficient algorithms and a computer for this. It would take quite, quite some times for a human to figure out this.

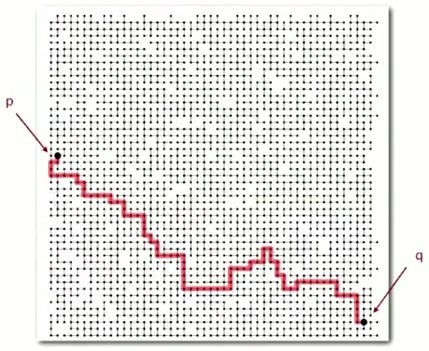
In this case, there is a connection.

Applications (How to model the problem?)

Applications involve manipulating objects of all types:

• Pixels in a digital photo
• Computers in a network
• Friends in a social network
• Transistors in a computer chip
• Elements in a mathematical set
• Variable names in Fortran program
• Metallic sites in a composite system.

For programming, it is convenient to name objects 0 to N-1

• Use integers as array index
• Suppress details not relevant to union-find. (We use symbol table to translate from site names to integers.)

Modeling the connections

We assume "is connected to" is an equivalent relation:

• Reflexive: p is connected to p.
• Symmetric: if p is connected to q, then q is connected to p.
• Transitive: if p is connected to q and q is connected to r, then p is connected to r.

Connected components. Maximal set of objects that are mutually connected.

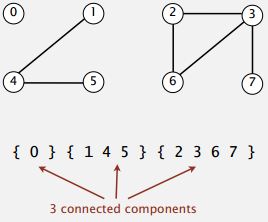
Implementing the operations

• Find query: check if two objects are in the same component.
• Union command: replace components containing two object with their union.

So, for example, if we have these components, and we get the command to union connect, 2 and 5. Essentially, we need to merge the connected components containing the one containing 2 or the one containing 5 to get a big connected components and now we have only two connected components.

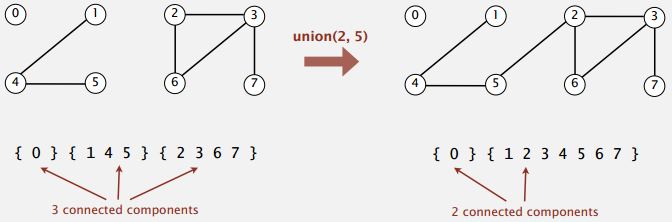
Union-find data type (API)

Goal: design efficient data structure for union-find

• Number of objects N can be huge
• Number of operations M can be huge
• Find queries and union commands may be intermixed.

References & Resources

• N/A