Introduction

Quick-find and Quick-union are introduced. Both of which are easy to implement. But simply can't support a huge dynamic connectivity problems. So, how we are going to do better?

Improvement 2: Path Compression

Just after computing the root of p, set the id of each examined node to point to that root.

This is the idea of path compression. And this idea is, when we're trying to find the root of the tree containing a given node. We're touching all the nodes on the path from that node to the root. While we're doing that we might as well make each one of those just point to the root. There's no reason not to.

So when we're trying to find the root of P. After we find it, we might as well just go back and make every node on that path just point to the root (As shown in the Figure below).

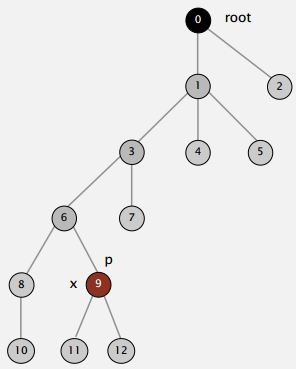
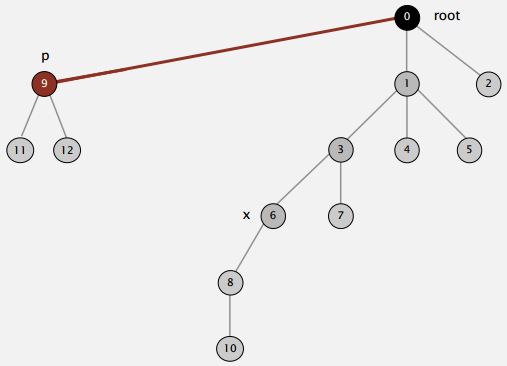
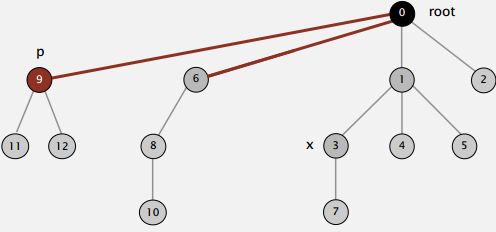
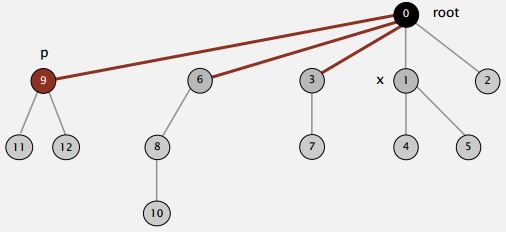
That's going to be a constant extra cost. We went up the path once to find the root. Now, we'll go up again to just flatten the tree out. And the reason would be, no reason not to do that. We had one line of code to flatten the tree, amazingly.

Actually to make a one liner code, we use a simple variant where we make every other node in the path point to its grandparent on the way up the tree. Now, that's not quite as good as totally flattening actually in practice that it actually is just about as good. So, with one line of code, we can keep the trees almost completely flat.

Now, this algorithm people discovered rather early on after figuring out the weighting and it turns out to be fascinating to analyze quite beyond our scope. But we mentioned this example to illustrate how even a simple algorithm, can have interesting and complex analysis. And what was proved by Hopcroft Ulman and Tarjan was that if you have N objects, any sequence of M union and find operations will touch the array at most a c (N + M lg * N) times.

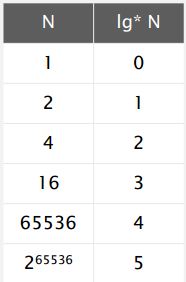
And now, lg N is kind of a funny function. It's the number of times you have to take the log of N to get one. And the way to think, it's called the iterated log function. And in the real world, it's best to think of that as a number less than five because lg two^ 65536 is five. So, that means that the running time of weighted quick union with path compression is going be linear in the real world and actually could be improved to even a more interesting function called the Ackermann function, which is even more slowly growing than lg . And another point about this is it< /i> seems that this is so close to being linear that is t ime proportional to N instead of time proportional to N times the slowly growing function in N. Is there a simple algorithm that is linear? And people, looked for a long time for that, and actually it works out to be the case that we can prove that there is no such algorithm. So, there's a lot of theory that goes behind the algorithms that we use. And it's important for us to know that theory and that will help us decide how to choose which algorithms we're going to use in practice, and where to concentrate our effort in trying to find better algorithms. It's amazing fact that was eventually proved by Friedman and Sachs, that there is no linear time algorithm for the union find problem. But weighted quick union with path compression in practice is, is close enough that it's going to enable the solution of huge problems. So, that's our summary for algorithms for solving the dynamic connectivity problem. With using weighted quick union and with path compression, we can solve problems that could not otherwise be addressed. For example, if you have a billion operations and a billion objects I said before it might take thirty years. We can do it in six seconds. Now, and what's most important to recognize about this is that its the algorithm design that enables the solution to the problem. A faster computer wouldn't help much. You could spend millions on a super computer, and maybe you could get it done in six years instead of 30, or in two months but with a fast logarithm, you can do it in seconds, in seconds on your own PC.

References & Resources

• N/A