Introduction

Huge applications

• Percolatoin
• Games
• Dynamic connectivity
• Least common ancestor
• Equivalence of finite state automata
• Hoshen-kopelman algorithm in physics
• Hinley-Milner polymorphic type inference
• Kruskal's minimum spanning tree algorithm
• Compiling equivalence statements in Fortran
• Morphological attribute openings and closings
• Matlab's bwlabel() function in image processing.

Percolation - example

A model for many physical systems:

• N-by-N grid of sites
• Each site is open with probability p (or blocked with probability 1-p), open site is represented White and blocked is represented Black.
• System percolates if top and bottom are connected by open sites

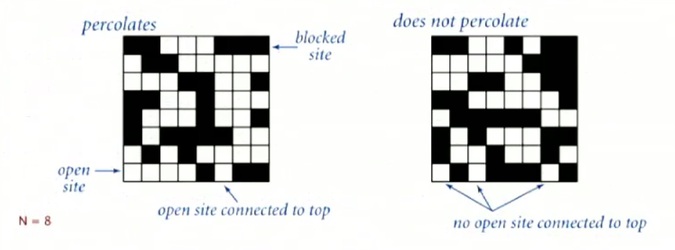
This is the model for many systems:

• You can think of for electricity. You could think of a vacant site as being a conductor, and a block site as being insulated. And so if there's a conductor from top to bottom then the thing conducts electricity.
• Or, you could think of it as water flowing through a porous substance of some kind. Where a vacant side is just empty and a block side has got some material, and either the water flows through from top to bottom, or not.
• Or you could think of a social network where it's people connected and either there's a connection between two people or not and these are a way not to get from one group of people to another communicating through that social network.

That's just a few examples of the percolation model, as listed in the table below.

So Let us look at the image below, if we are talking about a randomized model where the sites are vacant with the given probability.

And so it's pretty clear that if it's probability that a site is vacant is low as on the left, two examples on the left in this diagram, it's not going to percolate. There's not enough open site for there to be a connection from the top to the bottom. If the probability is high and there is a lot of open sides, it definitely is going to percolate. There would be lots of ways to get from the top to the bottom. But in the middle, when it's medium, it's questionable whether it percolates or not. So the scientific question, or the mathematical question from this model is, how do we know whether it's going to percolate or not?

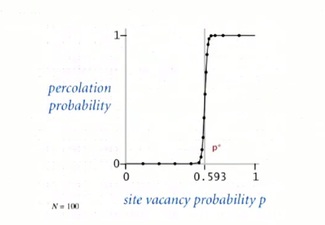
In this problem and in many similar problems, there's what's called a phase transition. Which says that, you know when it's low, it's not going to percolate. When it's high, it is going to percolate. And actually, the threshold between when it percolates and when it doesn't percolate is very sharp, as shown in the figure below.

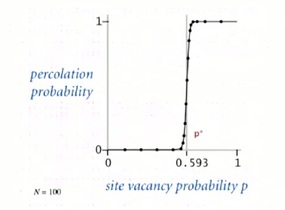
When N is large, theory guarantees a sharp threshold p*

• p > p*: almost certainly percolates
• p < p*: almost certainly does not percolate

Question is: What is the value of p* ?

And there is a value as N that if you're less than N it almost certainly will not percolate, if you're greater it almost certainly will. The question is what is that value. This is an example of a mathematical model where the problem is very well articulated. What's that threshold value, but nobody knows the solution to that mathematical problem. The only solution we have comes from a computational model, where we run simulations to try and determine the value of that probability. And those simulations are only enable by fast union find algorithms, that's our motivating example for why we need fast union find algorithms.

Monte Carlo simulation

We're going to run is called a so called Monte Carlo simulation. Where we initialize the whole grid to be block with all black and then we randomly fill in open sites.

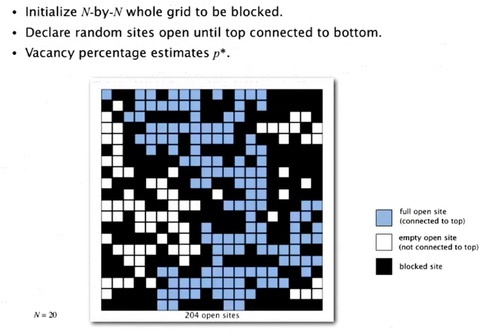
And we keep going. And every time we add an open site, we check to see if it makes the system percolate. And we keep going until we get to a point where the system percolates. And we can show that the vacancy percentage at the time that it percolates is an estimate of this threshold value. So what we want to do is run this experiment millions of times, which we can do in a computer, as long as we can, efficiently do the calculation of does it percolate or not. That's a Monte Carlo simulation, a computational problem that gives us a solution to this, scientifc problem where, mathematical problems nobody knows how to solve yet.

So, let's, look in a little bit more detail of how we're going to use our dynamic connectivity model to do this. So, we'll create an object corresponding to each site. And we'll give them a name, from zero to N^2-1 as indicated here.

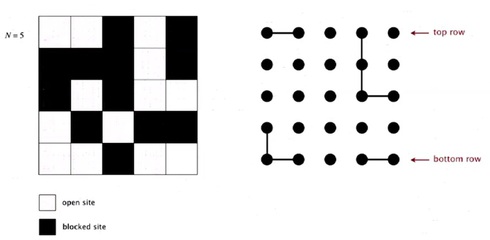
Percolates if any site on bottom row is connected to site on top row. A clever trick is to introduce 2 virtual sites (and connections to top and bottom). So that, it percolates if virtual top site is connected to virtual bottom site.

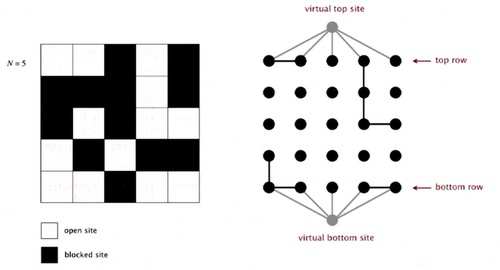
And then we'll connect them together. If they're connected by open sites. So the percolation model on the left corresponds to the, connection model on the right, according to what we've been doing.

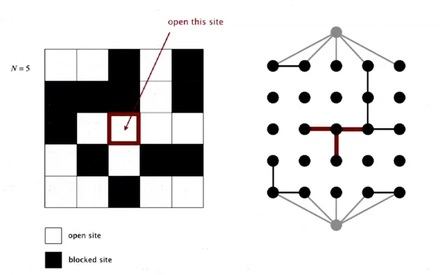
So, how do to model opening a new site? It is simply mark new site as open then connect it to all of its adjacent open sites.

By running enough simulations for a big-enough n, that this, percolation threshold is about .592746. With this fast algorithm we can get an accurate answer to the scientific question. If we use a slow Union-find algorithm we won't be able to run it for very big problems and we won't get a very accurate answer.

References & Resources

• N/A