Introduction

In physics, the angular velocity is a vector quantity (more precisely, a pseudo-vector) which specifies the angular speed of an object and the axis about which the object is rotating. The Unit (Metric System) of angular velocity is radians per second,  although it may be measured in other units such as degrees per second, revolutions per second, revolutions per minute, degrees per hour, etc. It is sometimes also called the rotational velocity and its magnitude the rotational speed, typically measured in cycles or rotations per unit time (e.g. revolutions per minute). Angular velocity is usually represented by the symbol omega (ω, rarely Ω).

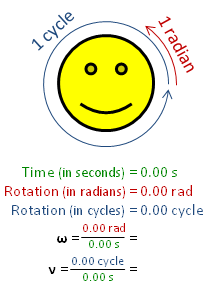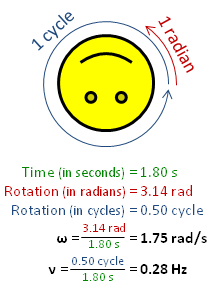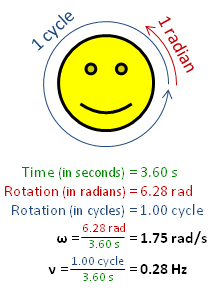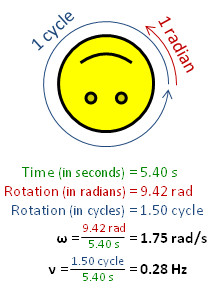
The radian per second is defined as the change in the orientation of an object, in radians, every second.

Angular frequency ω	(Ordinary) frequency ν = ω / 2π
2π radians per second	exactly 1 hertz (Hz)
1 radian per second	approximately 0.159155 Hz
1 radian per second	approximately 57.29578 degrees per second
1 radian per second	approximately 9.5493 revolutions per minute

Others - Radian

Radian describes the plane angle subtended by a circular arc as the length of the arc divided by the radius of the arc. One radian is the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle. More generally, the magnitude in radians of such a subtended angle is equal to the ratio of the arc length to the radius of the circle; that is, θ = s /r, where θ is the subtended angle in radians, s is arc length, and r is radius. Conversely, the length of the enclosed arc is equal to the radius multiplied by the magnitude of the angle in radians; that is, s = rθ. A complete revolution is 2π radians (shown here with a circle of radius one and circumference 2π).

It follows that the magnitude in radians of one complete revolution (360 degrees) is the length of the entire circumference divided by the radius, or 2πr /r, or 2π. Thus 2π radians is equal to 360 degrees, meaning that one radian is equal to 180/π degrees.

References & Resources

• Wikipedia - http://en.wikipedia.org/wiki/Angular_velocity
• Wikipedia - http://en.wikipedia.org/wiki/Radians_per_second