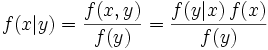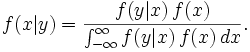Bayes theorem

  1. Home
  2. Maths
  3. Fundamentals

Introduction

In probability theory, Bayes’ theorem (also known as Bayes’ rule) is a useful tool for calculating conditional probabilities.

bayes

In Bayes’ theorem, each probability has a conventional name:

  • P(B│A) is the conditional probability of B, given A. It is also called the likehood.
  • P(A) is the prior probability of A.
  • P(B) is the prior probability of B.
  • P(A│B) is the conditional probability of A, given B. It is also called the posterior probability because it is derived from or depends upon the specified value of B.

To derive Bayes’ theorem

It is quite obvious to know the following two conditions:

bayes theorem

bayes theorem

Then, P(A│B)P(B)=P(A∩B)=P(B│A)P(A), and finally, we get:

bayes theorem

Extension

Extension 1:

bayes theorem

Note: P(B,C)= P(B∩C) is the probability of the interaction of B and C.

Extension 2:

bayes theorem

For probability densities

There is also a version of Bayes' theorem for continuous distributions. It is somewhat harder to derive, since probability densities, strictly speaking, are not probabilities, so Bayes' theorem has to be established by a limit process; see Papoulis (citation below), Section 7.3 for an elementary derivation. Bayes' theorem for probability densities is formally similar to the theorem for probabilities:

f(x|y) = rac{f(x,y)}{f(y)} = rac{f(y|x),f(x)}{f(y)} !

and there is an analogous statement of the law of total probability:

f(x|y) = rac{f(y|x),f(x)}{int_{-infty}^{infty} f(y|x),f(x),dx}. !

As in the discrete case, the terms have standard names. f(x, y) is the joint distribution of X and Y, f(x|y) is the posterior distribution of X given Y=y, f(y|x) = L(x|y) is (as a function of x) the likelihood function of X given Y=y, and f(x) and f(y) are the marginal distributions of X and Y respectively, with f(x) being the prior distribution of X.

Here we have indulged in a conventional abuse of notation, using f for each one of these terms, although each one is really a different function; the functions are distinguished by the names of their arguments.

References & Resources

  • http://en.wikipedia.org/wiki/Bayes%27_theorem
  • http://mathworld.wolfram.com/BayesTheorem.html
  • Athanasios Papoulis (1984). Probability, Random Variables, and Stochastic Processes, second edition. New York: McGraw-Hill.

Latest Post