Gradient in Vector Calculus

  1. Home
  2. Maths
  3. Fundamentals

Introduction

In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of the scalar field, and whose magnitude is that rate of increase. In simple terms, the variation in space of any quantity can be represented by a slope. The gradient represents the steepness and direction of that slope.

Definition

The gradient of a function f(x1, x2, x3, ... , xn) is denoted ∇ f or where ∇ ( the nabla symbol ) denotes the vector differential operator.

In a rectangular coordinate system, the gradient is the vector field whose components are the partial derivatives of f :

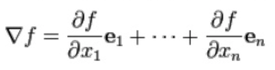
Gradient in Vector Calculus

For example, the gradient of the function:

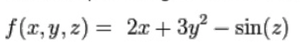
Gradient in Vector Calculus

is:

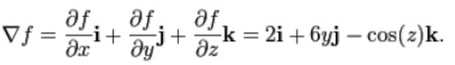
Gradient in Vector Calculus

References & Resources

  • http://en.wikipedia.org/wiki/Gradient

Latest Post