Introduction

In mathematics, a real number is a value that represents a quantity along a continuous line. The real numbers include all the rational numbers, such as the integer -5 and the fraction 4/3, and all the irrational numbers such as √2 (=1.141421..., the square root of two) and π (3.1415926..., a transcendental number).

Notation

Mathematicians use the symbol R (or alternatively, 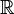, the letter "R" in blackboard bold, Unicode ℝ– U+211D) to represent the set of all real numbers (as this set is naturally endowed with a structure of field, the expression field of the real numbers is more frequently used than set of all real numbers). The notation Rⁿ refers to the Cartesian product of n copies of R, which is an n-dimensional vector space over the field of the real numbers; this vector space may be identified to the n-dimensional space of Euclidean geometry as soon as a coordinate system has been chosen in the latter. For example, a value from R³ consists of three real numbers and specifies the coordinates of a point in 3-dimensional space.

In mathematics, real is used as an adjective, meaning that the underlying field is the field of the real numbers (or the real field). For example real matrix, real polynomial and real Lie algebra. As a substantive, the term is used almost strictly in reference to the real numbers themselves (e.g. The "set of all reals").

References & Resources

• http://en.wikipedia.org/wiki/Real_number