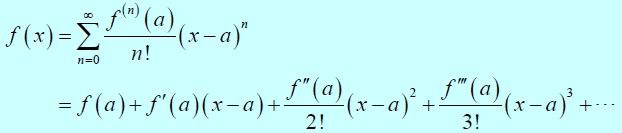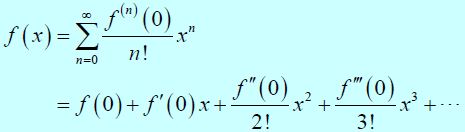Introduction

In this section we discussed a power series representation of a function. The problem with the approach in that section is that everything came down to needing to be able to relate the function in some way to:

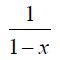
and while there are many functions out there that can be related to this function there are many more that simply can't be related to this.

So, without taking anything away from the process we looked at in the previous section, what we need to do is come up with a more general method for writing a power series representation for a function.

So, for the time being, let's make two assumptions. First, let's assume that the function f(x) does in fact have a power series representation about x = a,

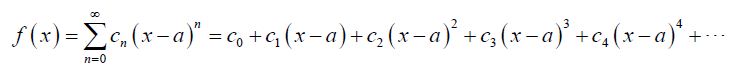
Next, we will need to assume that function, f(x), has derivatives of every order and that we can in fact find them all.

Now that we've assumed that a power series representation exists we need to determine what the coefficients, c_n, are. This is easier than it might at first appear to be. Let's first just evaluate everything at x = a. This gives,

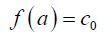
So, all the terms except the first are zero and we now know what c₀ is. Unfortunately, there isn't any other value of x that we can plug into the function that will allow us to quickly find any of the other coefficients. However, if we take the derivative of the function (and its power series) then plug in x=a we get,

and we now know c₁.

Let’s continue with this idea and find the second derivative.

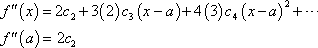
So, it looks like,

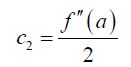
Using the third derivative gives,

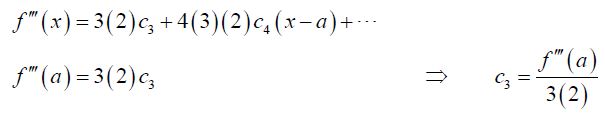
Using the fourth derivative gives,

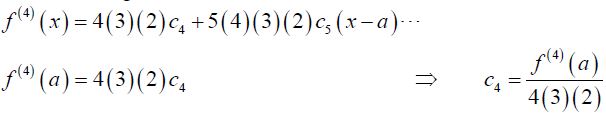
Hopefully by this time you’ve seen the pattern here. It looks like, in general, we’ve got the following formula for the coefficients.

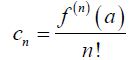
This even works for n=0 if you recall that 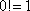and define .

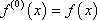So, provided a power series representation for the function f(x) about x=a exists the Taylor Series for f(x) about x=a is,

Taylor Series

If we use a=0, so we talking about the Taylor Series about x=0, we call the series a Maclaurin Series for f(x),

Maclaurin Series

Before working any examples of Taylor Series we first need to address the assumption that a Taylor Series will in fact exist for a given function. Let’s start out with some notation and definitions that we’ll need.

To determine a condition that must be true in order for a Taylor series to exist for a function let’s first define the n^th degree Taylor polynomial of f(x) as,

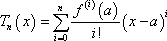
Note that this really is a polynomial of degree at most n! If we were to write out the sum without the summation notation this would clearly be an n^th degree polynomial. We’ll see a nice application of Taylor polynomials in the next section.

Notice as well that for the full Taylor Series,

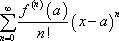
the n^th degree Taylor polynomial is just the partial sum for the series.

Next, the remainder is defined to be,

So, the remainder is really just the error between the function f(x) and the n^th degree Taylor polynomial for a given n.

With this definition note that we can then write the function as,

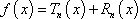
We now have the following Theorem.

References & Resources

• http://tutorial.math.lamar.edu/Classes/CalcII/TaylorSeries.aspx