Example 1

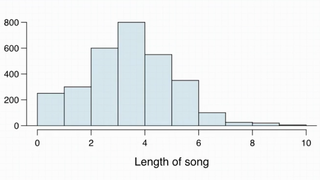
This is the same thing as saying among all the population of songs on this iPod, what percentage of them last more than 5 minutes. It seems we can calculate Z-score and the associated normal probabilities to find probability. However, this distribution is not nearly normal, it is indeed right-skewed (Because there is no upper end to how long your songs can be).

Note: To use Z-scores and the associated normal probabilities, you need to make sure the distribution we work with is nearly normal.

To do this, we need to make some educated guess:

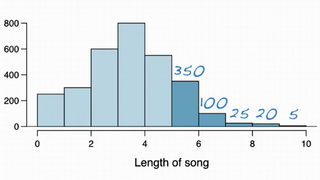
Therefore,

                      350 + 100 + 25 + 20 + 5    500
P(song length > 5) = ------------------------ = ----- = 0.17
                          3000                  3000

So, 17% of songs in my iPod last more than 5 minutes

Example 2

We know 6 hours is 360 minutes, so we need 360 minutes worth of songs. Therefore, we can write this question to

P( X1 + X2 + X3 + ... + X100 > 360 min) = ? 

This is equivalent to the average length > 3.6 minutes:

P( x̄ > 3.6 ) = ? 

The central limit theorem says that x̄ will be distributed nearly normally when mean = population mean, which is 3.45 minutes. And with standard error equal to the population standard deviation σ divided by √n

                              σ    1.63
x̄ ~ N (mean = μ = 3.45, SE = --- = ----- = 0.163)
                             √n    √100

So, we draw the curve and we are looking for everything above that:

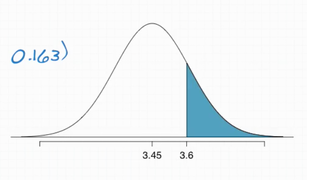
Next, we calculate the Z score:

      3.6 - 3.45
Z = ------------- = 0.92
        0.163

After that, we can easily find the probability using central limit theorem, R or web app.

P( X > 0.92 ) = 0.179

So there is about 18% chance that my playlist lasts at least the entire drive.

References & Resources;

• N/A