Introduction

The Sugeno Fuzzy model (also known as the TSK fuzzy model) was proposed by Takagi, Sugeno, and Kang in an effort to develop a systematic approach to generating fuzzy rules from a given input-output dataset. A typical fuzzy rule in a Sugeno fuzzy model has the form:

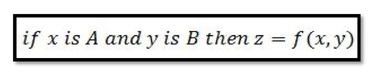
where A and B are fuzzy sets in the antecedent, while z=f(x,y) is a crisp function in the consequent. Usually f(x, y) is a polynomial in the input variables x and y, but it can be any function as long as it can appropriately describe the output of the model within the fuzzy region specified by the antecedent of the rule. When f(x, y) is a first-order polynomial, the resulting fuzzy inference system is called a first-order Sugeno fuzzy model, which was originally proposed in [1, 2]. When f is a constant, we then have a zero-order Sugeno fuzzy model, which can be viewed either as a special case of the Mamdani Fuzzy inference system, in which each rule’s consequent is specified by a fuzzy singleton (or a pre-defuzzified consequent), or a special case of the Tsukamoto fuzzy model, in which each rule’s consequent is specified by an MF of a step function centre at the constant. Moreover, a zero-order Sugeno fuzzy model is functionally equivalent to a radial basis function network under certain minor constraints, as discussed in Chapter 12 in “Neuro-fuzzy and soft computing”.

The output of a zero-order Sugeno model is a smooth function of its input variables as long as the neighbouring MFs in the antecedent have enough overlap. In other words, the overlap of MFs in the consequent of a Mamdani model does not have a decisive effect on the smoothness; it is the overlap of the antecedent MFs that determines the smoothness of the resulting input-output behaviour.

Figure 1: 1st order Sugeno Fuzzy Model

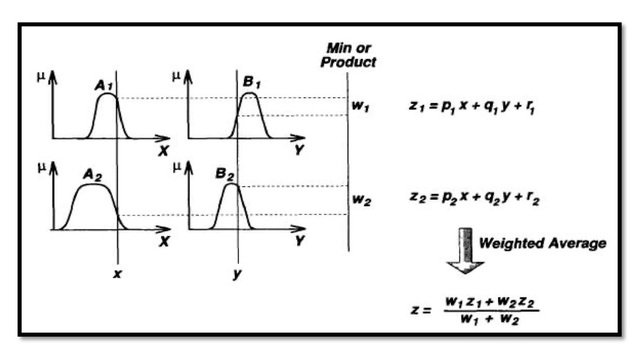
Figure 1 shows the fuzzy reasoning procedure for a first-order Sugeno fuzzy model. Since each rule has a crisp output, the overall output is obtained via weighted average, thus avoiding the time-consuming process of defuzzification required in a Mamdani model. In practice, the weighted average operator is sometimes replaced with the weighted sum operator (that is, z=w₁z₁ + w₂z₂ in Figure 1) to reduce computation further, especially in the training of a fuzzy inference system. However, this simplification could lead to the loss of MF linguistic meanings unless the sum of firing strengths (that is, ∑_iw_i ) is close to unity. Since the only fuzzy part of a Sugeno model is in its antecedent, it is easy to demonstrate the distinction between a set of fuzzy rules and nonfuzzy ones.

Example 1: Fuzzy and nonfuzzy rule set – a comparison

An example of a single-input Sugeno fuzzy model can be expressed as:

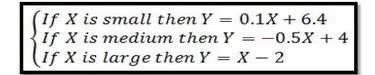
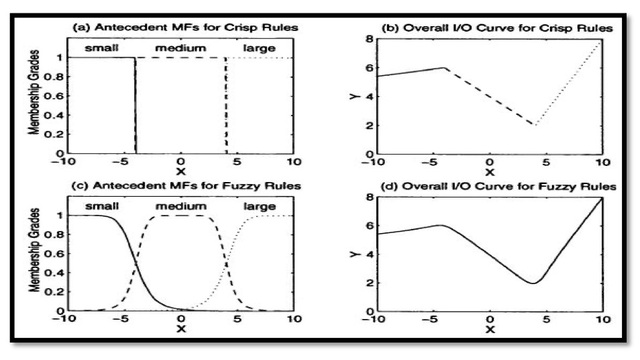
If “small”, “medium”, and “large” are nonfuzzy sets with membership functions shown in Figure 2(a), then the overall input-output curve is piecewise linear, as shown in Figure 2(b). On the other hand, if we have smooth membership functions instead, the overall input-output curve become a smoother one, as shown in Figure 2(d).

Figure 2: Comparison between fuzzy and nonfuzzy rules: (a) Antecedent MFs and (b) input-output curve for nonfuzzy rules; (c) Antecedent MFs and (d) input-output curve for fuzzy rules.

Sometimes a simple Sugeno fuzzy model can generate complex behaviour. The following is an example of a two-input system.

Example 2: Two-input single-output Sugeno fuzzy model

An example of a two-input single-output Sugeno fuzzy model with four rules can be expressed as:

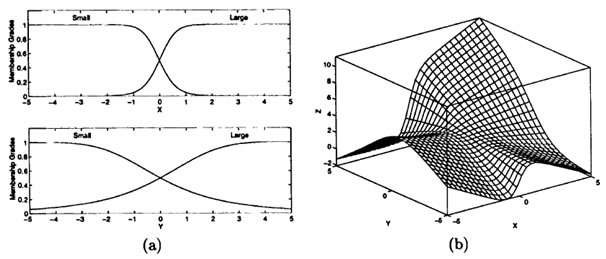
Figure 3(a) plots the membership functions of input X and Y, and Figure 3(b) is the resulting input-output surface. The surface is complex, but it is till obvious that the surface is composed of four planes, each of which is specified by output equation of a fuzzy rule.

Figure 3: Two-input single-output Sugeno fuzzy model: (a) antecedent and consequent MFs; (b) overall input-output surface.

Unlike the Mamdani fuzzy model, the Sugeno fuzzy model cannot follow the compositional rule of inference strictly in its fuzzy reasoning mechanism. This poses some difficulties when the inputs to a Sugeno fuzzy model are fuzzy. Specifically, we can still employ the matching of fuzzy sets, as shown in the antecedent part of Figure 1, to find the firing strength of each rule. However, the resulting overall output via either weighted average or weighted sum is always crisp; this is counterintuitive since a fuzzy model should be able to propagate the fuzziness from inputs to outputs in an appropriate manner.

Without the time-consuming and mathematically intractable defuzzification operation, the Sugeno fuzzy model is by far the most popular candidate for sample-data-based fuzzy modelling.

References & Resources

• Chapter 4 in "Neuro-fuzzy and soft computing"
• [1] M. Sugeno and G.T. Kang, Structure identification of Fuzzy Model
• [2] T. Takagi and M. Sugeno, Fuzzy identification of systems and its applications to modeling and control.