Introduction

In the Tsukamoto fuzzy models, the consequent of each fuzzy if-then rule is represented by a fuzzy set with a monotonical membership function, as shown in Figure 1. As a result, the inferred output of each rule is defined as a crisp value induced by the rule’s firing strength. The overall output is taken as the weighted average of each rule’s output. Figure 1 illustrates the reasoning procedure for a two-input two-rule system.

Figure 1: The Tsukamoto fuzzy model

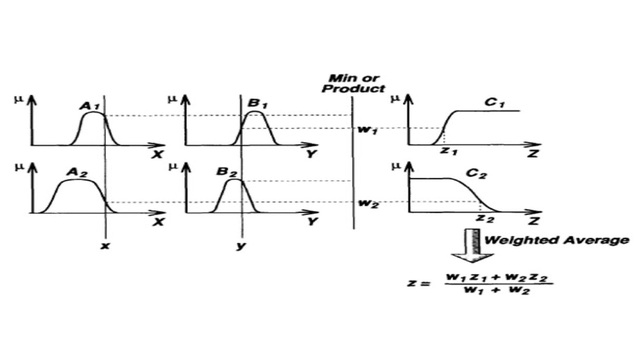
Since each rule infers a crisp output, the Tsukamoto fuzzy model aggregate each rule’s output by the method of weighted average and thus avoids the time-consuming process of defuzzification. However, the Tsukamoto fuzzy model is not used often since it is not as transparent as either the Mamdani or Sugeno fuzzy models. The following is a single-input example.

Example: Single-input Tsukamoto fuzzy model

An example of a single-input Tsukamoto fuzzy model can be expressed as:

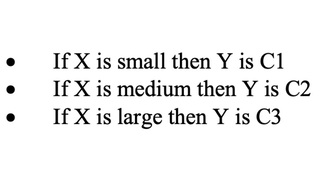
Where the antecedent MFs for “small”, “medium”, and “large” are shown in Figure 2(a), and the consequent MFs for “C₁”, “C₂”, and “C₃” are shown in Figure 2(b). The overall input-output curve, as shown in Figure 2(d), is equal to, where f_i is the output of each rule induced by the firing strength W_i and MF for C_i. If we plot each rule’s output f_i as a function of x, we obtain Figure 2(c), which is not quite obvious from the original rule base and MF plots.

Figure 2: Single-input single output Tsukamoto fuzzy model: (a) antecedent MFs; (b) consequent MFs; (c) each rule’s output curve; (d) overall input-output curve.

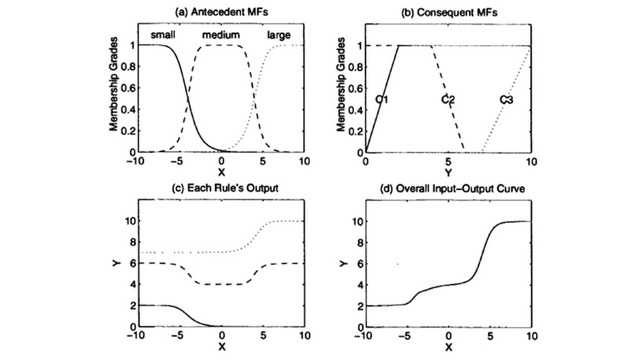
Since the reasoning mechanism of the Tsukamoto fuzzy model does not follow strictly the compositional rule of inference, the output is always crisp even when the inputs are fuzzy.

References & Resources

• "Neuro-fuzzy and soft computing"