Introduction

Quick-find and Quick-union are introduced. Both of which are easy to implement. But simply can't support a huge dynamic connectivity problems. So, how we are going to do better?

Improvement 1: weighting

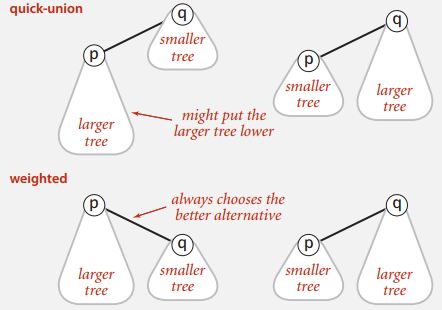
A very effective algorithm is called weighting. The idea is to when implementing the quick union algorithm take steps to avoid having tall trees. If you've got a large tree and a small tree to combine together what you want to try to do is avoid putting the large tree lower, that's going to lead to long tall trees. And there's a relatively easy way to do that. What we'll do is we'll keep track of the number of objects in each tree and then, we'll maintain balance by always making sure that we link the root of the smaller tree to the root of the larger tree.

So, as shown in Figure 1, we avoid this first situation here where we put the larger tree lower. In the weighted algorithm, we always put the smaller tree lower.

Weighted quick-union

• Modify quick-union to avoid tall trees
• Keep track of size of each tree (number of objects)
• Balance by linking root of smaller tree to root of larger tree

Figure 1: weighted quick-union

Weighted quick-union demo

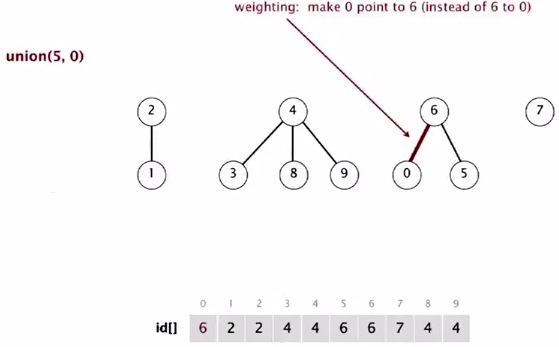
Union(5, 0)

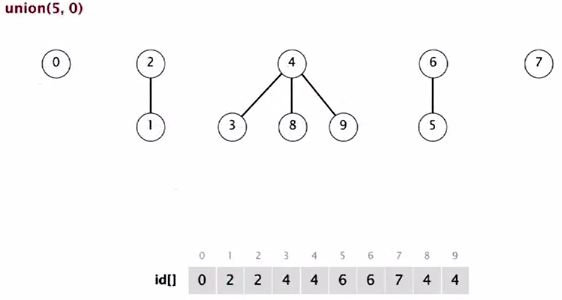
5 in a bigger tree, so 0 goes below

Union(7, 2)

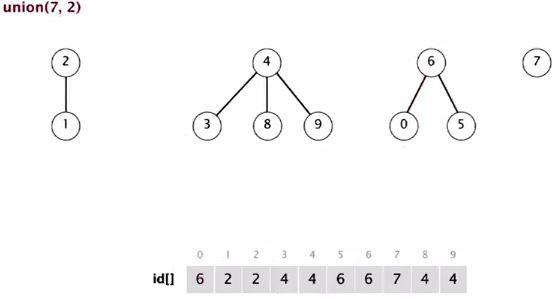
2 in a bigger tree, so 7 goes below.

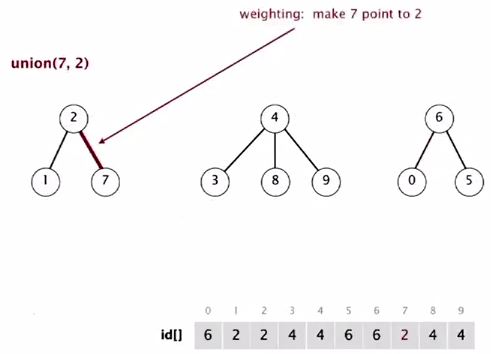
Union(6, 1)

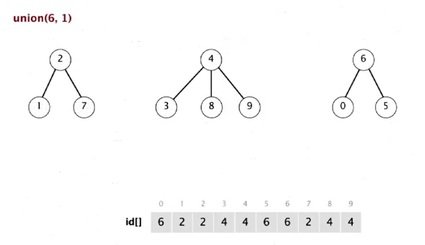
They are equal size tree.

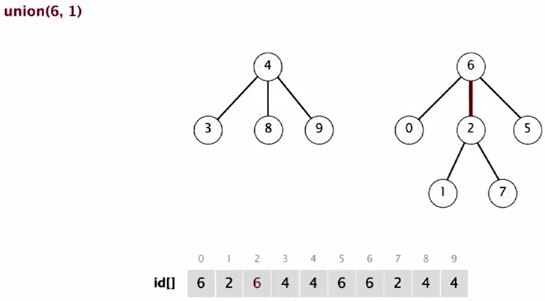
Union(7, 3)

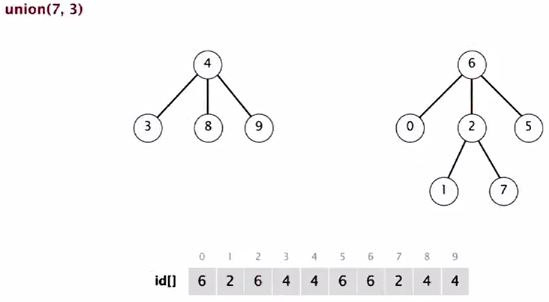
3 in a small tree and it goes below.

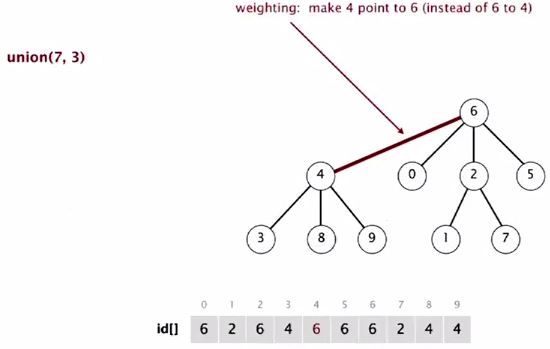
Then, we end up with a single tree representing all the objects. But this time, we have some guarantee that no item is too far from the root.

Effect example

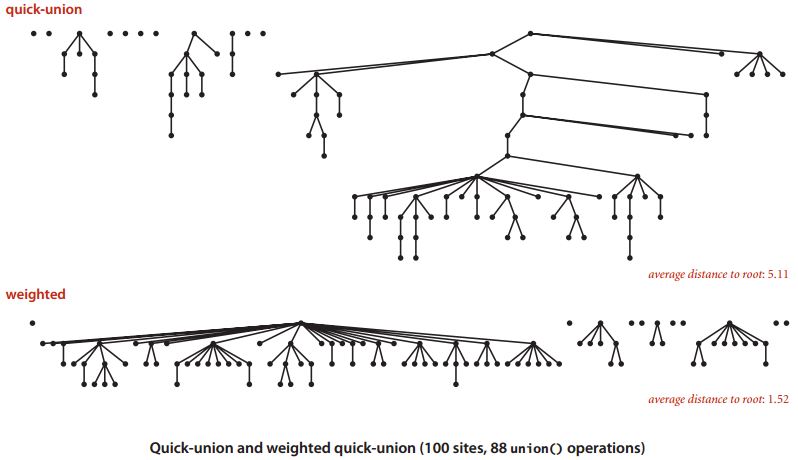
Here is an example that shows the effect of doing the weighted quick union where we always put the smaller tree down below for the same set of union commands. This is with a hundred sites and 88 union operations. You can see in the top the big tree has some trees, some nodes, a fair distance from the root. In the bottom, for the weighted algorithm all the nodes are within distance four from the root. The average distance to the root is much, much lower.

Weighted quick-union: Java implementation

Data Structure: Same as quick-union, but maintain extra array sz[i] to count number of objects in the tree rooted at i.

Find operation: identical to quick-union

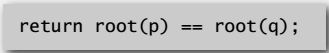
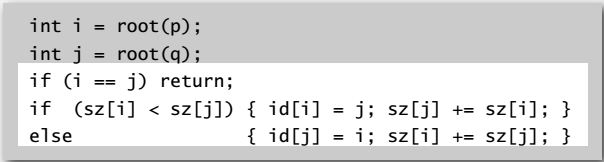
Union operation: modify quick-union to:

• Link root of smaller tree to root of larger tree
• Update the sz[] array

Weighted quick-union analysis

Running time:

• Find operation: takes time proportional to depth of p and q.
• Union operation: takes constant time, given roots.

Proposition: Depth of any node x is at most lgN, as shown in Figure below. (lg is base 2 logarithm)

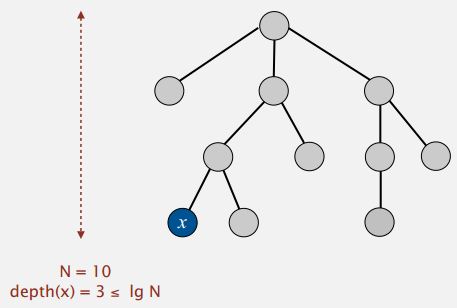
Proof to above proposition:

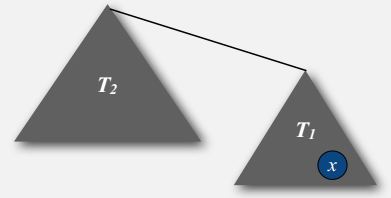
When does depth of x increase?

Increases by 1 when tree T1 containing x is merged into another tree T2.

• The size of the tree containing x at least doubles since |T2| >= |T1|
• Size of tree containing x can double at most lgN times.

Detailed Explanation: The x's depth will increase by one, when its tree, T1 in this diagram, is merged into some other tree, T2 in this diagram. At that point we said we only do that if the size of T2 was bigger than the or equal to size of T1. So, when the depth of x increases, the size of its tree at least doubles. So, that's the key because that means the size of the tree containing x can double at most logN times because if you start with one and double logN times, you get N and there's only N nodes in the tree. So, that's a sketch of a proof that the depth of any node x is at most log base two of N. And that has profound impact on the performance of this algorithm.

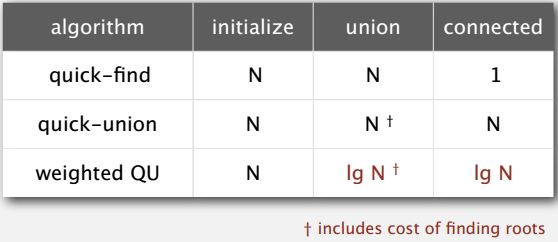
Now instead of the initialization always takes time proportional to N. But both the union and the connected or find operation takes time proportional to log base two of N. And that is an algorithm that scales. If N grows from a million to a billion, that cost goes from twenty to 30, which is quite not acceptable. Now, this was very easy to implement and, and we could stop but usually, what happens in the design of algorithms is now that we understand what it is that gains performance, we take a look and see, well, could we improve it even further. And in this case, it's very easy to improve it much, much more. And that's the idea of path compression.

References & Resources

• N/A