Introduction

The Mamdani fuzzy inference system was proposed as the first attempt to control a steam engine and boiler combination by a set of linguistic control rules obtained from experienced human operators. Figure 1 is an illustration of how a two-rule Mamdani fuzzy inference system derives the overall output z when subjected to two crisp inputs x and y.

Figure 1: The Mamdani fuzzy inference system using min and max for T-norm and T-conorm operators, respectively

If we adopt max and algebraic product as our choice for the T-norm and T-conorm operators, respectively, and use max-product composition instead of the original max-min composition, then the resulting fuzzy reasoning is shown in Figure2, where the inferred output of each rule is a fuzzy set scaled down by its firing strength via algebraic product. Although this type of fuzzy reasoning was not employed in Mamdani's original paper, it has often been used in the literature. Other variations are possible if we use different T-norm and T-conorm operators.

Figure 2: The Mamdani fuzzy inference system using product and max for T-norm and T-conorm operators, respectively

In Mamdani's application [1], two fuzzy inference systems were used as two controllers to generate the heat input to the boiler and throttle opening of the engine cylinder, respectively, to regulate the steam pressure in the boiler and the speed of the engine. Since the plant takes only crisp values as inputs, we have to use a defuzzifier to convert a fuzzy set to a crisp value.

Defuzzification

Defuzzification refers to the way a crisp value is extracted from a fuzzy set as a representative value. In general, there are five methods for defuzzifying a fuzzy set A of a universe of discourse Z, as shown in Figure 3. (Here the fuzzy set A is usually represented by an aggregated output MF, such as C' in Figures 4.2 and 4.3).

Figure 3: Various defuzzification schemes for obtaining a crisp output

A brief explanation of each defuzzification strategy are shown as follows:

• Centroid of area z_COA:
  

  

  
  where μ_A(z) is the aggregationed output MF. This is the most widely adopted defuzzification strategy, which is reminiscent of the calculation of expected values of probability distributions.
• Bisector of area z_BOA: z_BOA satisfies

  

  
  where α=min{z|z ∈ Z} and β=max{z|z ∈ Z}. That is, the vertical line z=z_BOA partitions the region between z=α, z=β, y=0 and y=μ_A(z) into two regions with the same area.
• Mean of maximum z_MOM: z_MOM is the average of the maximizing z at which the MF reach a maximum μ*. In symbols

  

  
  where Z' = {z | μ_A(z)=μ*}. In particular, if μ_A(z) has a single maximum at z=z*, then z_MOM=z*. Moreover, if μ_A(z) reaches its maximum whenever z ∈ [z_left, z_right] (This is the case in Figure 3), then zMOM = (z_left + z_right)/2. The mean of maximum is the defuzzification strategy employed in Mamdani's fuzzy logic controllers.
• Smallest of maximum z_SOM: z_SOM is the minimum (in terms of magnitude) of the maximizing z.
• Largest of maximum z_LOM: z_LOM is the maximum (in terms of magnitude) of the maximizing z. Because of their obvious bias, z_SOM and z_LOM are not used as often as the other three defuzzification methods.

The calculation needed to carry out any of these five defuzzification operations is time-consuming unless special hardware support is available. Furthermore, these defuzzification operations are not easily subject to rigorous mathematical analysis, so most of the studies are based on experimental results. This leads to the propositions of other types of fuzzy inference systems that do not need defuzzification at all; two of them are introduced:

• Sugeno Fuzzy Models (Also known as Takagi-Sugeno or TSK Fuzzy Model);
• Tsukamoto Fuzzy Models ;

Example 1: Single-input single-output Mamdani fuzzy model

An example of a single-input single-output Mamdani fuzzy model with three rules can be expressed as:

Figure 3

Figure 4

Figure 3 plots the membership functions of input X and output Y, where the input and output universe are [-10, 10] and [0, 10], respectively. With maxmin composition and centroid defuzzification, we can find the overall input-output curve, as shown in Figure 4. Note that the output variable never reaches the maximum (10) and minimum (0) of the output universe. Instead, the reachable minimum and maximum of the output variable are determined by the centroids of the leftmost and rightmost consequent MFs, respectly.

Example 2: Two-input single-output Mamdani fuzzy model

An example of a two-input single-output Mamdani fuzzy model with four rules can be expressed as:

Figure 5

Figure 6

Figure 5 plots the membership functions of input X and Y and output Z, all with the same universe [-5, 5]. With max-min composition and centroid defuzzification, we can find the overall input-output surface, as shown in Figure 6. For a multiple-input fuzzy model, sometimes it is helpful to have a tool for viewing the process of fuzzy inference; Figure 7 is the fuzzy inference viewer available in the Matlab Fuzzy Logic Toolbox, where you can change the input values by click and drag the input vertical lines and then see the interactive changes of qualified consequent MFs and overall output MF.

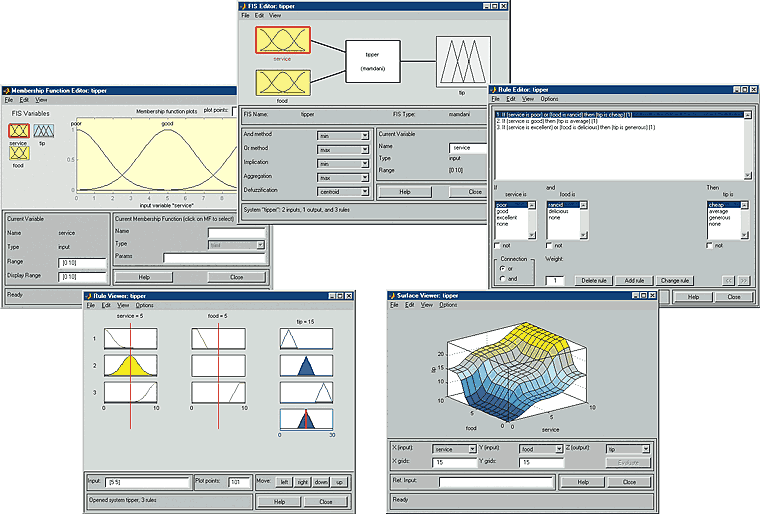
Figure 7

References & Resources

• Book - Neuro Fuzzy and soft computing
• [1] E.H. Mamdani and S. Assilian. An experiment in linguistic synthesis with a fuzzy logic controller. International Journal of Man-Machine Studies, 7(1):1-13. 1975