Introduction

In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector-valued function. Specifically, suppose 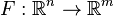is a function which takes as input real n-tuples and produces as output real m-tuples. Such a function is given by m real-valued component functions, 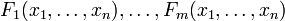. The partial derivatives of all these functions with respect to the variables 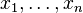(if they exist) can be organised in an m-by-n matrix, the Jacobian matrix J of F, as follows:

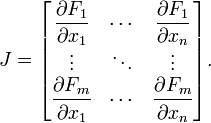
This matrix, whose entries are functions of 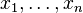, is also denoted by 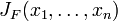and .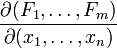

(Note that some books define the Jacobian as the transpose of the matrix given above.)

The relation between Jacobian matrix and Gradient:

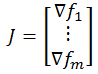
The Jacobian matrix is important because if the function F is differentiable at a point p=(x1, ... , xn), which is a slightly stronger condition than merely requiring that all partial derivatives exist there, then the derivative of F at p is the linear transformation 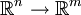represented by the matrix 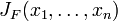. This linear transformation is the best linear approximation of the function F near the point p.

In the case m=n, the Jacobian matrix will be a square matrix, and its determinant, a function of x1, ... , xn, is the Jacobian determinant of F. It carries important information about the local behavior of F and can be thought of as a local expansion factor for volumes; it is used when performing variable substitutions in multi-variable integrals since it occurs prominently in the substitution rule for multiple variables.

A Simple Example

Consider the function 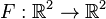given by

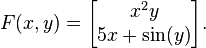
Then we have

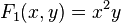
and

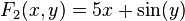
and the Jacobian matrix of F is

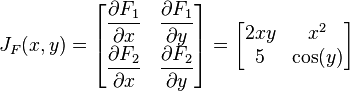
and the Jacobian determinant is

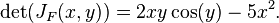
References & Resources

• http://en.wikipedia.org/wiki/Jacobian_matrix