Singular and Non-singular Matrix
Definition of Non-singular Matrix
If the determinant of a matrix is not equal to zero, then the matrix is called a non-singular matrix.
More about Non-singular Matrix
An n x n(square) matrix A is called non-singular if there exists an n x n matrix B such that AB = BA = In, where In, denotes the n x n identity matrix.
If the matrix is non-singular, then its inverse exists.
Properties of non-singular matrix:
- If A and B are non-singular matrices of the same order, then AB is non-singular.
- If A is non-singular, then Ak is non-singular for any positive integer k.
- If A is non-singular and k is a non-zero scalar, then kA is non-singular.
Example of Non-singular Matrix
The determinant of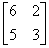 
i.e. 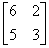= 6(3) – 5(2) = 18 - 10 = 8 ≠ 0, so it is a non-singular matrix.
References & Resources
- N/A
Latest Post
- Dependency injection
- Directives and Pipes
- Data binding
- HTTP Get vs. Post
- Node.js is everywhere
- MongoDB root user
- Combine JavaScript and CSS
- Inline Small JavaScript and CSS
- Minify JavaScript and CSS
- Defer Parsing of JavaScript
- Prefer Async Script Loading
- Components, Bootstrap and DOM
- What is HEAD in git?
- Show the changes in Git.
- What is AngularJS 2?
- Confidence Interval for a Population Mean
- Accuracy vs. Precision
- Sampling Distribution
- Working with the Normal Distribution
- Standardized score - Z score
- Percentile
- Evaluating the Normal Distribution
- What is Nodejs? Advantages and disadvantage?
- How do I debug Nodejs applications?
- Sync directory search using fs.readdirSync