What is Normal Probability Plot

The normal probability plot is a graphical technique for assessing whether or not a data set is approximately normally distributed.

The data are plotted against a theoretical normal distribution in such a way that the points should form an approximate straight line. Departures from this straight line indicate departures from normality.

Sample Plot

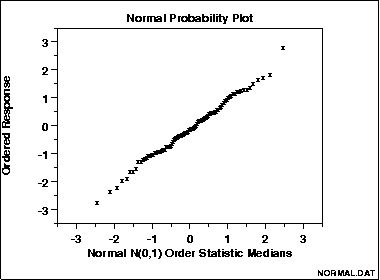
The points on this plot form a nearly linear pattern, which indicates that the normal distribution is a good model for this data set.

How to form Normal Probability Plot

The normal probability plot is formed by:

• Vertical axis: ordered response values;
• Horizontal axis: normal order statistic medians;

The observations are plotted as a function of the corresponding normal order statistic medians which are defined as:

Ni = G(Ui)

where U_i are the uniform order statistic medians (defined below) and G is the percent point function of normal distribution.

Percent Point Function

The percent point function is the inverse of the cumulative distribution function (probability that x is less than or equal to some value). That is, given a probability, we want the corresponding x of the cumulative distribution function.

Uniform Order Statistic Medians

The uniform order statistic medians can be approximated by:

Ui = 1 - Un    for i = 1
Ui = (i - 0.3175)/(n + 0.365)    for i = 2, 3, ..., n-1 
Ui = 0.5(1/n)    for i = n

In addition, a straight line can be fit to the points and added as a reference line. The further the points vary from this line, the greater the indicatioin of departures from normality.

What Normal Probability Plot can answer?

The normal probability plot is used to answer the following questions:

1. Are the data normally distributed?
2. What is the nature of the departure from normality (data skewed, shorter than expected tails, longer than expected tails)?

Examples

1. Data are normally distributed;
2. Data have short tails;
3. Data have fat tails;
4. Data are skewed right;

References & Resources

• N/A