Introduction

There are certain common issues concerning all the three fuzzy inference systems introduced previously, such as how to partition an input space and how to construct a fuzzy inference system for a particular application.

Input Space Partitioning

Now it should be clear that the spirit of fuzzy inference systems resembles that of “divide and conquer” – the antecedent of a fuzzy rule defines a local fuzzy region, while the consequent constituent can be a consequent MF (Mamadani and Tsukamoto Fuzzy models), a constant value (zero-order Sugeno model), or a linear equation (first-order Sugeno model). Different consequent constituents result in different fuzzy inference systems, but their antecedents are always the same. Therefore, the following discussion of methods of partitioning input spaces to form the antecedents of fuzzy rules is applicable to all three types of fuzzy inference systems.

Figure 1: Various methods for partitioning the input space: (a) grid partition; (b) tree partition; (c) scatter partition.

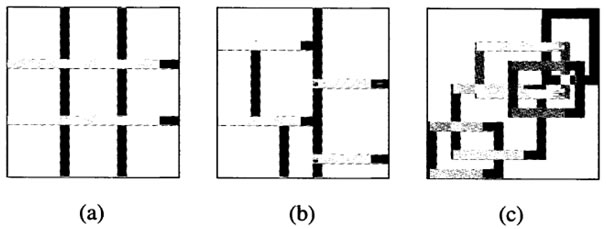
• Grid partition: Figure 1(a) illustrates a typical grid partition in a two-dimensional input space. This partition method is often chosen in designing a fuzzy controller, which usually involves only several state variables as the inputs to the controller. This partition strategy needs only a small number of MFs for each input. However, it encounters problems when we have a moderately large number of inputs. For instance, a fuzzy model with 10 inputs and 2 MFs on each input would result in 2^10=1024 fuzzy if-then rules, which is prohibitively large. This problem, usually referred to as the curse of dimensionality, can be alleviated by the other partition strategies.
• Tree partition: Figure 1(b) shows a typical tree partition, in which each region can be uniquely specified along a corresponding decision tree. The tree partition relieves the problem of an exponential increase in the number of rules. However, more MFs for each input are needed to define these fuzzy regions, and these MFs do not usually bear clear linguistic meanings such as “small”, “big”, and so on. In other words, orthogonality holds roughly in X×Y, but not in either X or Y alone. Tree partition is used by the CART (classification and regression tree) algorithm.
• Scatter partition: As shown in Figure 1(c), by covering a subset of the whole input space that characterises a region of possible occurrence of the input vectors, the scatter partition can also limit the number of rules to a reasonable amount. However, the scatter partition is usually dictated by desired input-output data pairs and thus, in general, orthogonality does not hold in X, Y or X×Y. This makes it hard to estimate the overall mapping directly from the consequent of each rule’s output.

Note that Figure 1 is based on the assumption that MFs are defined on the input variables directly. If MFs are defined on certain transformations of the input variables, we could end up in a more flexible partition style. Figure 2 is an example of the input partition when MFs are defined on linear transformations of the input variables.

Fuzzy Modeling

By now the reader should have already developed a clear picture of both the structures and operations of several types of fuzzy inference systems. In general, we design a fuzzy inference system based on the past known behaviour of a target system. The fuzzy system is then expected to be able to reproduce the behaviour of the target system. For example, if the target system is a human operator in charge of a chemical reaction process, then the fuzzy inference system becomes a fuzzy logic controller that can regulate and control the process. Similarly, if the target system is a medical doctor, then the fuzzy inference becomes a fuzzy expert system for medical diagnosis.

Let us now consider how we might construct a fuzzy inference system for a specific application. Generally speaking, the standard method for constructing a fuzzy inference system, a process usually called fuzzy modelling, has the following features:

• The rule structure of a fuzzy inference system makes it easy to incorporate human expertise about the target system directly into the modelling process. Namely, fuzzy modelling takes advantage of domain knowledge that might not be easily or directly employed in other modelling approaches.
• When the input-output data of a target system is available, conventional system identification techniques can be used for fuzzy modelling. In order words, the use of numerical data also plays an important role in fuzzy modelling, just as in other mathematical modelling methods.

In what follows, we shall summarize some general guidelines concerning fuzzy modelling. Specific examples of fuzzy modelling for various applications can be found in subsequent chapters. Conceptually, fuzzy modelling can be pursued in two stages, which are not totally disjoint. The first stage is the identification of the surface structure, which includes the following tasks:

1. Select relevant input and output variables;
2. Choose a specific type of fuzzy inference system;
3. Determine the number of linguistic terms associated with each input and output variables; (For a Sugeno model, determine the order of consequent equations.)
4. Design a collection of fuzzy if-then rules;

Note that to accomplish the preceding tasks, we rely on our own knowledge (common sense, simple physical laws, and so on) of the target system, information provided by human experts who are familiar with the target system (which could be the human experts themselves), or simply trial and error.

After the first stage of fuzzy modelling, we obtain a rule base that can more or less describe the behaviour of the target system by means of linguistic terms. The meaning of these linguistic terms is determined in the second stage, the identification of deep structure, which determines the MFs of each linguistic term (and the coefficients of each rule’s output polynomial if a Sugeno fuzzy model is used). Specifically, the identification of deep structure includes the following tasks:

1. Choose an appropriate family of parameterised MFs;
2. Interview human experts familiar with the target systems to determine the parameters of the MFs used in the rule base;
3. Refine the parameters of the MFs using regression and optimisation technique;

Task 1 and 2 assume the availability of human experts, while task 3 assumes the availability of a desired input-output data set. Various system identification and optimisation techniques for parameter identification in task 3 are. When a fuzzy inference system is used as a controller for a given plant, then the objective in task 3 should be changed to that of searching for parameters that will generate the best performance of the plant; this aspect of fuzzy logic controller design can be found in Chapter 17 and 18 of the book “Neuro-fuzzy and soft computing”.

References & Resources

• Chapter 4, Neuro-fuzzy and soft computing