Introduction

The Hessian Matrix is a square matrix of second-order partial derivatives of a function. It describes the local curvature of a function of many variables.

Defination from a function

Given the real-valued function f(x₁, x₂, ..., x_n), if all second partial derivatives of f exist and are continuous over the domain of the function, then the Hessian matrix of f is

where x = (x₁, x₂, ..., x_n) and D_i is the differentiation operator with respect to the ith argument. Thus

Defination from an existing Jacobian matrix

The Jacobian matrix of the derivatives 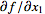, , 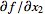..., 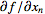of a function 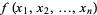with respect to x₁, x₂, ..., x_n is called the Hessian H of f, i.e.

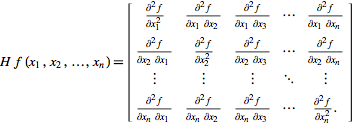
Applications

Hessian matrices are used in large-scale optimisation problems within Newton-type methods because they are the coefficient of the quadratic term of a local Taylor expansion of a function. That is

Vector-valued functions

If f is instead a function from 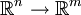,i.e.

then the array of second partial derivatives is not a two-dimensional matrix of size , but rather a tensor of order 3. This can be thought of as a multi-dimensional array with dimensions , which degenerates to usual Hessian matrix for m=1.

Note: The Vector-valued function can be found from Jacobian matrix.

References & Resources

• http://en.wikipedia.org/wiki/Hessian_matrix
• http://mathworld.wolfram.com/Hessian.html